Régression logistique¶
La régression linéaire est utilisée pour estimer la relation (linéaire) entre une variable réponse continue et un ensemble de variables explicatives. Cependant, lorsque la variable réponse est binaire (Oui/Non, 0/1, bon/mauvais …), la régression linéaire n’est pas appropriée. La régression logistique peut être une meilleure altrenative.
Soit un vecteur de caractéristiques \(X\) et une réponse qualitative \(Y\) prenant des valeurs dans l’ensemble \(C\), la tâche de classification consiste à construire une fonction \(C(X)\) qui prend en entrée le vecteur de caractéristiques \(X\) et prédit sa valeur pour \(Y\) ; c’est-à-dire que \(C(X) \in C\).
Nous sommes donc plus intéressés par l’estimation des probabilités que \(X\) appartienne à chaque catégorie de \(C\). Par exemple, pour une compagnie d’assurance, il est plus intéressant d’estimer la probabilité qu’une réclamation soit frauduleuse que de savoir si elle est frauduleuse ou non.
Considérons l’ensemble de données Default, où la variable réponse par default appartient à l’une des deux catégories suivantes : Yes ou No. Plutôt que de modéliser directement cette variable réponse \(Y\), la régression logistique modélise la probabilité que \(Y\) appartienne à une catégorie particulière. Avec ces données, nous allons illustrer le concept de classification. Nous souhaitons prédire si un individu sera en défaut de paiement sur sa carte de crédit, sur la base de son revenu annuel et du solde mensuel de sa carte de crédit.
Dans le graphique ci-dessous (code); nous avons représenté le revenu annuel et le solde mensuel des cartes de crédit pour un sous-ensemble de 10 000 personnes.
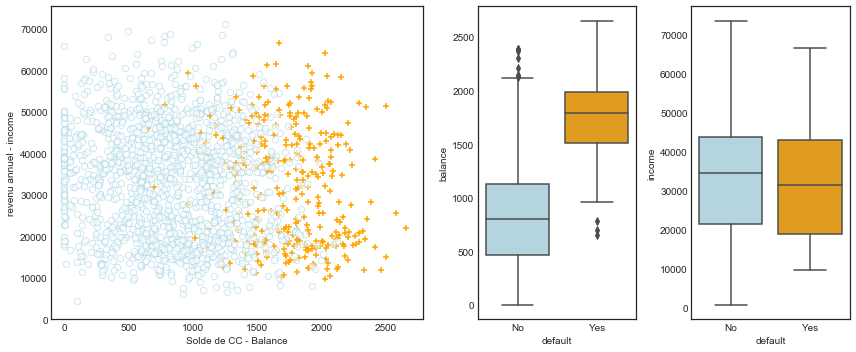
Les individus qui ont fait défaut au cours d’un mois donné sont représentés en orange, et ceux qui n’ont pas fait défaut en bleu.
Le taux de défaut de paiment global est d’environ 3 %, nous n’avons donc représenté qu’une fraction des personnes qui n’ont pas fait défaut. Il semble que les personnes qui ont manqué à leurs engagements aient eu tendance à avoir des soldes de carte de crédit plus élevés que celles qui n’ont pas manqué à leurs engagements.
la probabilité d’un défaut de paiement pour un solde donné peut s’écrire comme suit
Les valeurs de \(\operatorname{Pr}(\text { default }=\text { Yes } \mid \text { balance })\), que nous désignons p(balance), seront comprises entre 0 et 1. Ensuite, pour toute valeur donnée, une prédiction peut être faite pour le défaut de paiement.
Par exemple, on peut prédire que le default = Yes pour tout individu pour lequel p(balance) \(> 0,5\). Par ailleurs, si une entreprise souhaite être prudente dans la prédiction des individus qui risquent d’être en défaut, elle peut choisir d’utiliser un seuil plus bas, tel que p(balance) \(> 0,1\).
On peut bien penser d’appliquer une régression linéaire sur un tel exemple. Toutefois, cela peut donner des probbabilités \(>1\) ou même \(<0\). Voici un graphique (code) qui illustre cette situation;
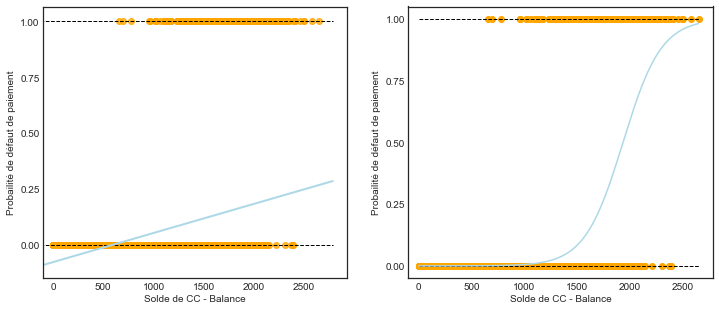
Où les \(0\) sont tracées en bas et les \(1\) en haut en orange. Sur le paneau gauche, on voit une ligne droite de la régression linéaire qui montre clairement certines valeurs inférieures à 0. Alors que sur le graphique de droite, nous avons appliqué une regression logistique qui semble donner de meilleures probabilité pour ce cas.
Régression logistique simple¶
Pour éviter ce problème, nous devons modéliser \(p(X)\) à l’aide d’une fonction qui donne des valeurs comprises entre \(0\) et \(1\) pour toutes les valeurs de \(X\).
Dans la régression logistique, nous utilisons la fonction logistique,
Les \(\beta_{i}\) paramètres représentent les coefficients comme dans la régression linéaire et \(p(X)\) peut être interprété comme la probabilité que la classe positive (défaut de paiement dans l’exemple ci-dessus) soit présente.
Le minimum pour \(p(X)\) est obtenu à \(\lim _{a \rightarrow-\infty}\left[\frac{e^{a}}{1+e^{a}}\right]=0\)
et le maximum pour \(p(X)\) est obtenu à \(\lim _{a \rightarrow \infty}\left[\frac{e^{a}}{1+e^{a}}\right]=1\) qui restreint les probabilités de sortie à 0-1.
En réarrangeant l’équation \(p(X)\), on obtient une équation linéaire similaire à la variable réponse moyenne dans un modèle de régression linéaire simple qu’on appel la transformation logit:
L’utilisation de la transformation logit donne également lieu à une interprétation intuitive de l’ampleur de \(\beta_{1}\) : les chances (par exemple, de défaillance) augmentent de manière multiplicative par \(\exp \left(\beta_{1}\right)\) pour chaque augmentation d’une unité de \(X\).
Estimations des Beta¶
Nous utilisons le maximum de vraisemblance pour estimer les paramètres.
Cette vraisemblance donne la probabilité des zéros et des uns observés dans les données. On choisit \(\beta_{0}\) et \(\beta_{1}\) pour maximiser la vraisemblance des données observées. La plupart des logiciels statistiques permettent d’ajuster des modèles de régression logistique linéaire par maximum de vraisemblance. Dans R, nous utilisons la fonction glm.
La regression logistique multiple¶
Nous pouvons également étendre notre modèle comme indiqué dans la régression logistique simple afin de pouvoir prédire une réponse binaire à l’aide de prédicteurs multiples :
Exemple¶
Les données¶
Nous utiliserons un ensemble de données qui illustre le endements quotidiens en pourcentage de l’indice boursier S&P 500 entre 2001 et 2005.
library(ISLR2)
head(Smarket)
| Year | Lag1 | Lag2 | Lag3 | Lag4 | Lag5 | Volume | Today | Direction | |
|---|---|---|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <fct> | |
| 1 | 2001 | 0.381 | -0.192 | -2.624 | -1.055 | 5.010 | 1.1913 | 0.959 | Up |
| 2 | 2001 | 0.959 | 0.381 | -0.192 | -2.624 | -1.055 | 1.2965 | 1.032 | Up |
| 3 | 2001 | 1.032 | 0.959 | 0.381 | -0.192 | -2.624 | 1.4112 | -0.623 | Down |
| 4 | 2001 | -0.623 | 1.032 | 0.959 | 0.381 | -0.192 | 1.2760 | 0.614 | Up |
| 5 | 2001 | 0.614 | -0.623 | 1.032 | 0.959 | 0.381 | 1.2057 | 0.213 | Up |
| 6 | 2001 | 0.213 | 0.614 | -0.623 | 1.032 | 0.959 | 1.3491 | 1.392 | Up |
dim(Smarket)
- 1250
- 9
summary(Smarket)
Year Lag1 Lag2 Lag3
Min. :2001 Min. :-4.922000 Min. :-4.922000 Min. :-4.922000
1st Qu.:2002 1st Qu.:-0.639500 1st Qu.:-0.639500 1st Qu.:-0.640000
Median :2003 Median : 0.039000 Median : 0.039000 Median : 0.038500
Mean :2003 Mean : 0.003834 Mean : 0.003919 Mean : 0.001716
3rd Qu.:2004 3rd Qu.: 0.596750 3rd Qu.: 0.596750 3rd Qu.: 0.596750
Max. :2005 Max. : 5.733000 Max. : 5.733000 Max. : 5.733000
Lag4 Lag5 Volume Today
Min. :-4.922000 Min. :-4.92200 Min. :0.3561 Min. :-4.922000
1st Qu.:-0.640000 1st Qu.:-0.64000 1st Qu.:1.2574 1st Qu.:-0.639500
Median : 0.038500 Median : 0.03850 Median :1.4229 Median : 0.038500
Mean : 0.001636 Mean : 0.00561 Mean :1.4783 Mean : 0.003138
3rd Qu.: 0.596750 3rd Qu.: 0.59700 3rd Qu.:1.6417 3rd Qu.: 0.596750
Max. : 5.733000 Max. : 5.73300 Max. :3.1525 Max. : 5.733000
Direction
Down:602
Up :648
library(psych)
Modélisation¶
La fonction glm() ajuste les modèles linéaires généralisés, une classe de modèles qui inclut la régression logistique et la régression linéaire simple comme cas particuliers.
La syntaxe de la fonction glm() est similaire à celle de lm(), sauf que nous devons passer l’argument family = "binomial" afin d’indiquer à R d’exécuter une régression logistique plutôt qu’un autre type de modèle linéaire généralisé.
glm.fits <- glm(Direction~Lag1 + Lag2 + Lag3 + Lag4 + Lag5 + Volume,
data = Smarket,
family = binomial,)
En arrière-plan, glm(), utilise l’estimation linéaire pour estimer les paramètres inconnus du modèle. L’intuition de base derrière l’utilisation de cette estimation pour ajuster un modèle de régression logistique est la suivante : nous cherchons des estimations pour \(\beta_{0}\) et \(\beta_{1}\) telles que la probabilité prédite \(\hat{p}\left(X_{i}\right)\) du rendement Up ou Down qui corresponde le plus possible au rendement de l’indiceboursier obbservé. En d’autres termes, nous essayons de trouver \(\beta_{0}\) et \(\beta_{1}\) de sorte que l’insertion de ces estimations dans le modèle pour \(p(X)\) donne un nombre proche de \(1\) pour tous les rendement Up, et un nombre proche de zéro pour tous les rendement Down.
Le tableau ci-dessous montre les estimations des coefficients et les informations connexes qui résultent de l’ajustement d’un modèle de régression logistique afin de prédire la probabilité du rendement de l’indice boursier.
summary(glm.fits)
Call:
glm(formula = Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 +
Volume, family = binomial, data = Smarket)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.446 -1.203 1.065 1.145 1.326
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.126000 0.240736 -0.523 0.601
Lag1 -0.073074 0.050167 -1.457 0.145
Lag2 -0.042301 0.050086 -0.845 0.398
Lag3 0.011085 0.049939 0.222 0.824
Lag4 0.009359 0.049974 0.187 0.851
Lag5 0.010313 0.049511 0.208 0.835
Volume 0.135441 0.158360 0.855 0.392
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1731.2 on 1249 degrees of freedom
Residual deviance: 1727.6 on 1243 degrees of freedom
AIC: 1741.6
Number of Fisher Scoring iterations: 3
La plus petite p-value ici est associée à Lag1. Le coefficient négatif de ce prédicteur suggère que si le marché a eu un rendement positif hier, il est moins probable qu’il augmente aujourd’hui. Cependant, avec une valeur de 0,15, p-value est encore relativement importante, et il n’y a donc pas de preuve évidente d’une association réelle entre Lag1 et Direction.
Rappelons que de petites valeurs p suggèrent qu’il est très peu probable que le coefficient réel soit nul, ce qui signifie qu’il est extrêmement peu probable que la caractéristique n’ait aucune relation avec la variable dépendante.
Nous utilisons la fonction coef() afin d’accéder uniquement aux coefficients de ce modèle ajusté.
print(coef(glm.fits))
(Intercept) Lag1 Lag2 Lag3 Lag4 Lag5
-0.126000257 -0.073073746 -0.042301344 0.011085108 0.009358938 0.010313068
Volume
0.135440659
Prédiction¶
La fonction predict() peut être utilisée pour prédire la probabilité que le marché monte, compte tenu des valeurs des prédicteurs. L’option type = "response" indique à R de sortir des probabilités de la forme P(Y = 1|X), par opposition à d’autres informations telles que le logit.
glm.probs <- predict(glm.fits, type = "response")
glm.probs[1:10]
- 1
- 0.507084133395401
- 2
- 0.481467878454591
- 3
- 0.481138835214201
- 4
- 0.515222355813022
- 5
- 0.510781162691538
- 6
- 0.506956460534911
- 7
- 0.492650874187038
- 8
- 0.509229158207377
- 9
- 0.517613526170958
- 10
- 0.488837779771376
Ici, nous avons affiché uniquement les dix premières probabilités
Afin de faire une prédiction sur la hausse ou la baisse du marché un jour donné, nous devons convertir ces probabilités prédites en étiquettes de classe, Hausse ou Baisse. Les deux commandes suivantes créent un vecteur de prédictions de classe selon que la probabilité prédite d’une hausse du marché est supérieure ou inférieure à 0,5.
glm.pred<-ifelse(glm.probs > .5, "Up", "Down")
glm.pred[1:10]
- 1
- 'Up'
- 2
- 'Down'
- 3
- 'Down'
- 4
- 'Up'
- 5
- 'Up'
- 6
- 'Up'
- 7
- 'Down'
- 8
- 'Up'
- 9
- 'Up'
- 10
- 'Down'
Évaluation de la précision du modèle¶
On peut alors utiliser une matrice de confusion tel qu’illustrée ci-dessous;
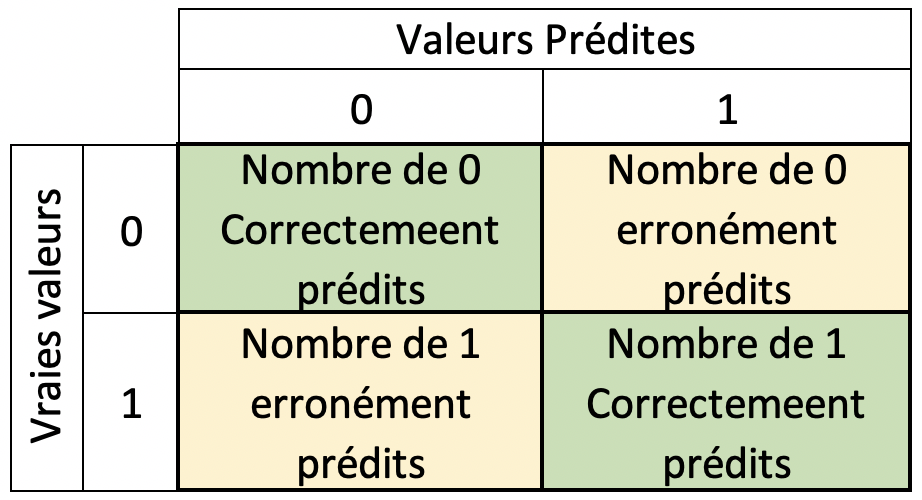
Fig. 9 Matrice de confusion¶
table(glm.pred, Smarket$Direction)
glm.pred Down Up
Down 145 141
Up 457 507
Les éléments diagonaux de la matrice de confusion indiquent les prédictions correctes, tandis que les éléments hors diagonale représentent les prédictions incorrectes.
Exactitude¶
Cette métique s’appelle la exactitude qui évalue combien de fois le classificateur est-il correct.
(507 + 145) / 1250
Sensibilité :¶
On définit la sensibilité comme étant la probabilité de détecter correctement un négatif, c’est-à-dire
Rappelons que les \(0\) sont le nombre de Down.
round(145/(457+141),4)
Spécificité¶
On définit la spécificité comme étant la probabilité de détecter correctement un positif, c’est-à-dire
Rappelons que les \(1\) sont le nombre de Up.
round(507/(141+507),4)
CARET pour évaluer de la précision¶
Le package R caret (Classification And REgression Training) est un ensemble de fonctions R qui facilite le processus de préparation des données pour la modélisation prédictive. Il contient d’autres fonctions qui permettent d’analyser les résultats de ces modèles. Par exemple, la fonction confusionMatrix permet d’obtenir les valeurs de la matrice de confusion.
library(caret)
Loading required package: lattice
matConfusion<-confusionMatrix(data = as.factor(glm.pred), reference =Smarket$Direction)
matConfusion
Confusion Matrix and Statistics
Reference
Prediction Down Up
Down 145 141
Up 457 507
Accuracy : 0.5216
95% CI : (0.4935, 0.5496)
No Information Rate : 0.5184
P-Value [Acc > NIR] : 0.4216
Kappa : 0.0237
Mcnemar's Test P-Value : <2e-16
Sensitivity : 0.2409
Specificity : 0.7824
Pos Pred Value : 0.5070
Neg Pred Value : 0.5259
Prevalence : 0.4816
Detection Rate : 0.1160
Detection Prevalence : 0.2288
Balanced Accuracy : 0.5116
'Positive' Class : Down
