Contents

Exercices

Laboratoires et exercices ISLR

Dans le manuel An introduction to statistical learning [JWHT13], vous pouvez faire les exercices suivants;

Laboratoires

  • 6.5.1 Subset Selection Methods

  • 6.5.2 Ridge Regression and the Lasso

Exercices ISLR

  • le #1) serait une bonne revision de la technique Subset Selection

  • le #2), #3) et #4) résume bien la théorie derrière Lasso, RSS et Ridge

  • le #6) pour pratique en R

  • le #8) a-b-e-f

  • le #9) a-b-c-d (nous ferons le (e) et (f) au prochain cours)

Cliquez sur le bouton pour la solution

Voici une proposition de solutions aux exercices du chapitre #6.

Exercices supplémentaires

Exercice 1

On vous donne la fonction de régression ajustée suivante d’un modèle de régression linéaire : $\( \hat{y}_{i}=.6100+9.9107 x_{i 1}+0.2893 x_{i 2}-2.2893 x_{i 3} \)$

  • a) Calculer la pénalité de rétraction (shrinkage penalty) sous la régression Ridge en utilisant le même paramètre de réglage \(\lambda_{\text{Ridge}}=5\).

    • rep:

  • b) Calculer la pénalité de rétraction (shrinkage penalty) sous la régression Lasso en utilisant le même paramètre de réglage \(\lambda_{\text{Lasso}}=5\).

Cliquez sur le bouton pour la solution

On se rappelle que le shrinkage penalty pour la régression Ridge est \(\lambda \sum_{j=1}^{p} \beta_{j}^{2}\) et pour Lasso il est \(\lambda \sum_{j=1}^{p}\left|\beta_{j}\right|\)

Cliquez sur le bouton ci-dessous pour le calcul numérique

beta_hat<-c(.6100,9.9107,0.2893,-2.2893)
lambda<-10

shrink_penal_Ridge<-lambda*sum(beta_hat**2)
shrink_penal_Ridge

shrink_penal_Lasso<-lambda*sum(abs(beta_hat))
shrink_penal_Lasso
1039.1866347
130.993

Exercice 2

Pour un ensemble de données comportant 999 observations, 2 prédicteurs \(\left(X_{1}\right.\) et \(\left.X_{2}\right)\), et une variable réponse \((Y)\), la somme des carrés résiduels a été calculée pour plusieurs estimations différentes d’un modèle linéaire avec un intercept \(\beta_{0}\). Seules les valeurs entières de 1 à 3 ont été considérées pour les estimations de \(\beta_{0}\) (l’ordonnée à l’origine), \(\beta_{1}\) et \(\beta_{2}\) tel qu’illustré dans les tableaux suivants:

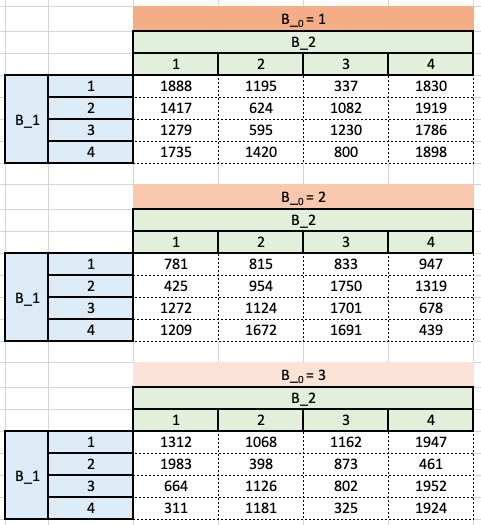
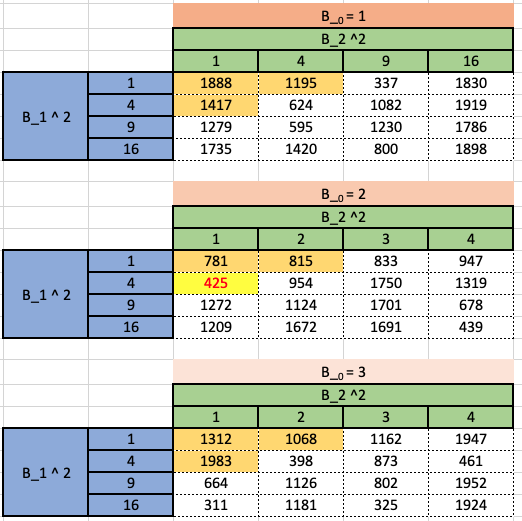
image.png

Soit \(\hat{\beta}_{j}^{R}\) l’estimation de \(\beta_{j}\) à l’aide d’une régression ridge avec la contrainte \(s=5.\)

Supposons que l’intercept ne soit pas soumis aux paramètres budgétaires. Quelles seront les \(\hat{\beta}_{j}^{R}\) que vous sélectionnerez pour votre modèle final?

Cliquez sur le bouton pour la solution

Puisque notre budget est \(\hat{\beta}_{1}^{2}+\hat{\beta}_{2}^{2} \leq 5\), le RSS le plus faible est obtenu lorsque \(\hat{\beta}_{0}=2, \hat{\beta}_{1}=2, \hat{\beta}_{2}=1\),

image.png

Exercice 3

Considérez les deux modèles de régression linéaire suivants :

\(\begin{array}{ll}y_{i}=12+2.13 x_{i 1}+6.03 x_{i 2}+\varepsilon_{i}, & \text { et } \sum \varepsilon_{i}^{2}=4.0 \\ y_{i}=11+1.0 x_{i 1}+0.1 x_{i 2}+\varepsilon_{i}, & \text { et } \sum \varepsilon_{i}^{2}=9.0\end{array}\)

Si la régression ridge est utilisée, pour quelles valeurs de \(\lambda\) le second modèle est-il préférable ?

Cliquez sur le bouton pour la solution

Après l’application de la pénalité de rétrécissement, la somme des carrés résiduels ajustée est la suivante

  • Pour le premier modèle: \(12+\left(2.13^{2}+6.03^{2}\right) \lambda=12+40.8978 \lambda\)

  • et pour le deuxième moèle: \(3+\left(.8^{2}+7.2^{2}\right) \lambda=3+52.48 \lambda\).

Ce qu’on veut c’est :

\(\begin{aligned} 3+52.48 \lambda < & 12+40.8978 \lambda \\ 11.5822 \lambda > & 9 \\ \lambda > & 0.777 \end{aligned}\)

JWHT13

Gareth James, Daniela Witten, Trevor Hastie, and Robert Tibshirani. An introduction to statistical learning. Volume 112. Springer, 2013.

Ridge Réduction des dimensions