Introduction à l’ACP¶
L’analyse en composantes principales est une méthode rapide de réduction de la dimension des données. Son comportement est plus facile à visualiser en examinant un ensemble de données bidimensionnelles. Considérez les 200 points suivants :
À l’oeil nu, il est clair qu’il existe une relation presque linéaire entre les variables \(x\) et \(y\). Cela rappelle les données de régression linéaire que nous avons vu, mais le problème posé ici est légèrement différent : plutôt que d’essayer de prédire les valeurs \(y\) à partir des valeurs \(x\), le problème d’apprentissage non supervisé tente de connaître la relation entre les valeurs \(x\) et \(y\).
Dans l’analyse en composantes principales, cette relation est quantifiée en trouvant une liste des axes principaux dans les données, et en utilisant ces axes pour décrire l’ensemble de données. En utilisant l’estimateur PCA de Scikit-Learn, nous pouvons calculer cela comme suit :
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X)
PCA(copy=True, iterated_power='auto', n_components=2, random_state=None,
svd_solver='auto', tol=0.0, whiten=False)
L’ajustement apprend certaines quantités à partir des données, surtout les “composantes” et la “variance expliquée” :
print(pca.components_)
[[-0.94446029 -0.32862557]
[-0.32862557 0.94446029]]
print(pca.explained_variance_)
[0.7625315 0.0184779]
Pour voir ce que ces nombres signifient, considérons-les comme des vecteurs sur les données d’entrée, en utilisant les “composantes” pour définir la direction du vecteur, et la “variance expliquée” pour définir la longueur au carré du vecteur :
plt.show()
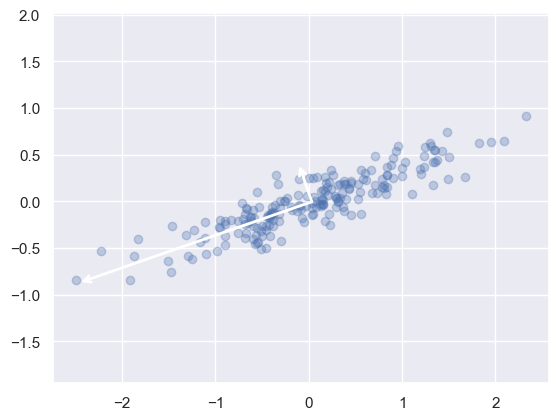
Ces vecteurs représentent les principaux axes des données, et la longueur du vecteur est une indication de l’importance de cet axe dans la description de la distribution des données - plus précisément, c’est une mesure de la variance des données lorsqu’elles sont projetées sur cet axe. La projection de chaque point de données sur les axes principaux sont les “composantes principales” des données.
Préserver la variance¶
Avant de pouvoir projeter l’ensemble de formation sur un hyperplan de dimension inférieure, vous devez d’abord choisir le bon hyperplan. Par exemple, un simple ensemble de données 2D est représenté à gauche de la figure ci-dessous, avec trois axes différents (c’est-à-dire des hyperplans unidimensionnels). À droite, on voit le résultat de la projection de l’ensemble de données sur chacun de ces axes. Comme vous pouvez le voir, la projection sur la ligne pleine préserve la variance maximale, tandis que la projection sur la ligne pointillée préserve une très faible variance, et la projection sur la ligne en tiret (au milieu) préserve une variance intermédiaire.
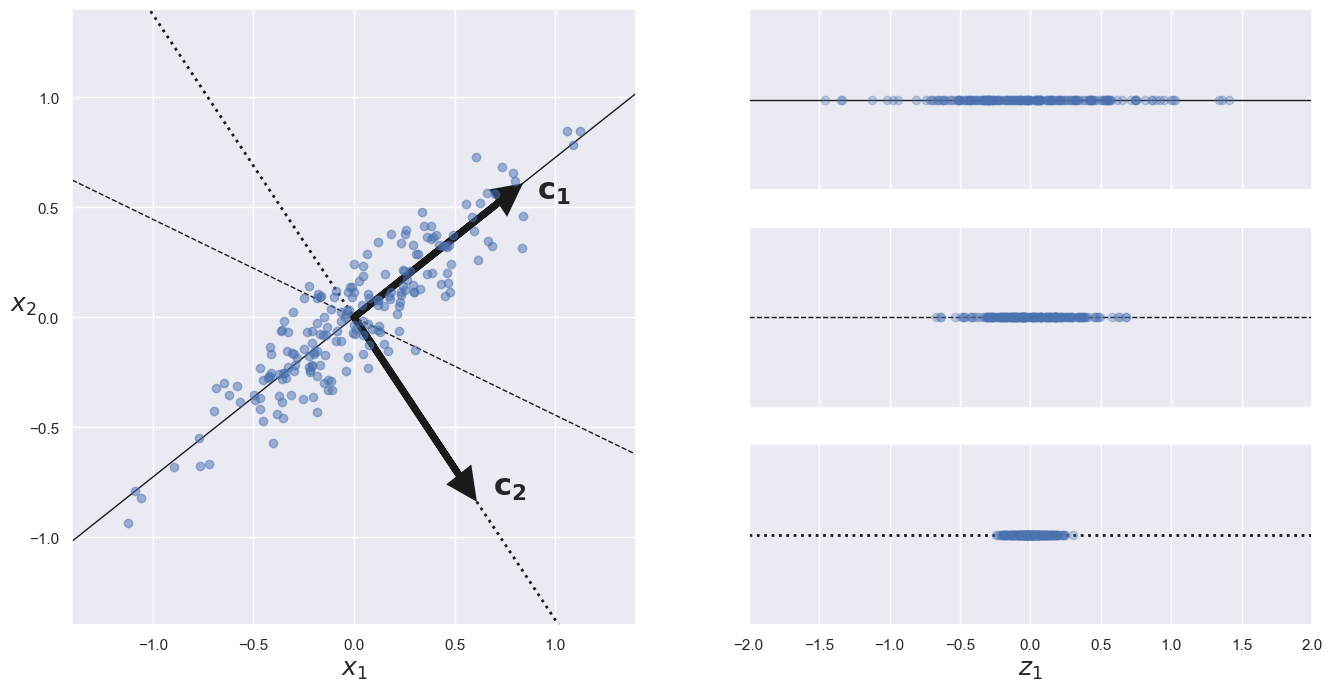
Il semble raisonnable de choisir l’axe qui préserve le maximum de variance, car il perdra très probablement moins d’informations que les autres projections. Une autre façon de justifier ce choix est que c’est l’axe qui minimise le carré moyen de la variance entre l’ensemble de données original et sa projection sur cet axe. C’est l’idée assez simple qui sous-tend l’ACP.
Composantes principales¶
L’ACP identifie l’axe qui représente la plus grande variance dans l’ensemble de l’entrainement. Dans la figure ci-dessus, il s’agit de la ligne continue. Elle trouve également un deuxième axe, orthogonal au premier, qui représente la plus grande variance restante. Dans cet exemple en 2D, ce deuxième choix c’est la ligne pointillée. S’il s’agissait d’un ensemble de données à dimensions supérieures, l’ACP trouverait également un troisième axe, orthogonal aux deux axes précédents, et un quatrième, un cinquième, et ainsi de suite, autant d’axes que le nombre de dimensions de l’ensemble de données.
Le vecteur unitaire qui définit le ième axe est appelé la ième composante principale. Dans la figure ci-dessus, la première CP est \(c_1\) et le 2ème CP est \(c_2\). Dans la figure ci-dessous, les deux première CP sont représentés par les flèches orthogonales dans le plan, et le troisième composante serait orthogonal au plan (pointant vers le haut ou vers le bas).
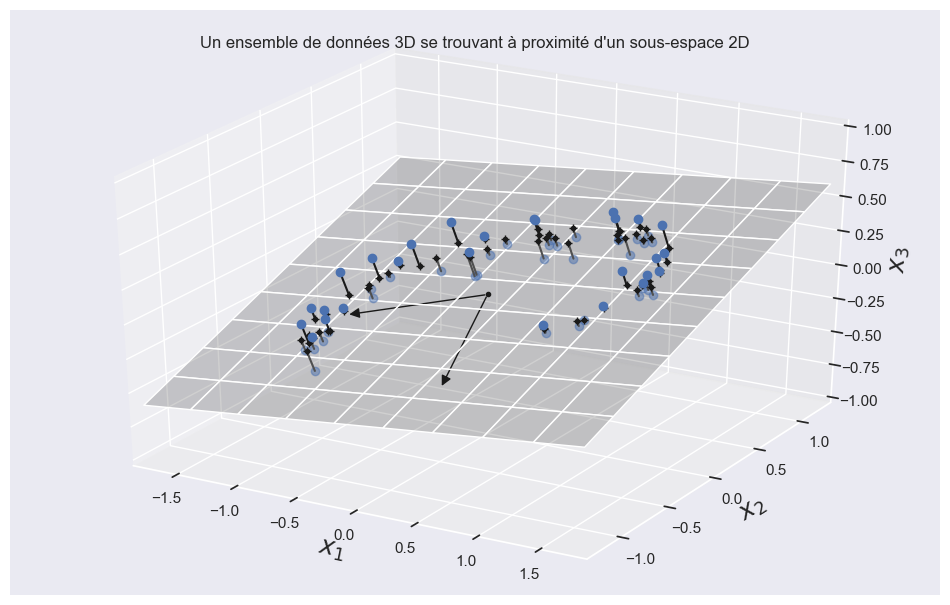
Ratio de variance expliqué¶
Combien de composantes principales faut-il utiliser ? Il n’y a pas de réponse définitive à cette question. Avec les méthodes supervisées, on répondrait à la question en utilisant la validation croisée. Mais cette méthode n’est pas disponible pour les méthodes non supervisées.
On peut considérer la proportion de variance expliquée (PVE) par les composantes principales. La variance totale des variables (que nous supposons toujours centrées sur 0 ) est de:
Si les variables sont normalisées (mises à l’échelle de sorte que leurs variances soient égales à 1 ), la variance totale est de \(p\).
La variance de la composante principale \(m^{\text {th }}\) est de:
En divisant \(\sum_{j=1}^{p} \operatorname{Var}\left(X_{j}\right)\) par \(\operatorname{Var}\left(Z_{m}\right)\) on obtient La PVE.
Exemple;¶
On vous donne pour deux variables aléatoires \(X_1\) et \(X_2\) sur 10 observations suivantes;
que \(\sum_{i=1}^{50} x_{i 1}^{2}=5610\) et \(\sum_{i=1}^{20} x_{i 2}^{2}=1520\), et que la variance pour la première composante principale \(Z_{1}\) est \(330.31\). On peut donc calculer la PVE, soit \([(5610+1520) / 20]/[330.31]\). Donc
X_1=[735,412,761,372,136,800,191,747,237,401]
X_2=[138,765,673,348,866,300,428,547,783,603]
On vous dit également que la variance pour la première composante principale \(Z_{1}\) est:
var_Z_1= 685460
Calculer la PVE.
On peut calculer d’abord \(\sum_{j=1}^{p} \operatorname{Var}\left(X_{j}\right)\);
Sum_Var_X_j=(np.sum(np.array(X_1)**2)+np.sum(np.array(X_2)**2))/10
Ensuite on divise pas \(\operatorname{Var}\left(Z_{m}\right)\);
Sum_Var_X_j/var_Z_1
0.9300001458874333
En Python, dans l’exmple 3D précédent, les rapports de variance expliqués des deux premières composantes de l’ensemble de données est données par la fonction explained_variance_ratio_;
print(pca.explained_variance_ratio_)
[0.84248607 0.14631839]
Cela vous indique que 84,2 % de la variance de l’ensemble de données se situe le long du premier axe, et 14,6 % le long du deuxième axe. Il reste donc moins de 1,2 % pour le troisième axe, ce qui permet de supposer qu’il contient probablement peu d’informations.
Choisir le bon nombre de dimensions¶
Au lieu de choisir arbitrairement le nombre de dimensions à réduire, il est généralement préférable de choisir le nombre de dimensions qui représentent une part suffisamment importante de la variance (par exemple 95%). À moins, bien sûr, que vous ne réduisiez la dimensionnalité pour la visualisation des données - dans ce cas, vous voudrez généralement réduire la dimensionnalité à 2 ou 3. Le code suivant calcule l’ACP sans réduire la dimensionnalité, puis calcule le nombre minimum de dimensions nécessaires pour préserver 95% de la variance de l’ensemble de formation :
pca = PCA()
pca.fit(X)
cumsum = np.cumsum(pca.explained_variance_ratio_)
d = np.argmax(cumsum >= 0.95) + 1
Vous pourriez alors définir n_components=d et relancer l’ACP. Cependant, il existe une bien meilleure option : au lieu de spécifier le nombre de composants principaux que vous souhaitez préserver, vous pouvez définir n_components comme un nombre entre 0,0 et 1,0, indiquant le ratio de variance que vous souhaitez préserver :
pca = PCA(n_components=0.95)
X_reduced = pca.fit_transform(X)
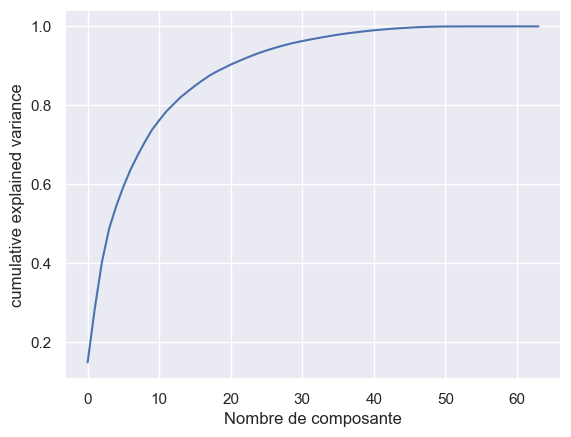
Une autre option encore consiste à tracer la variance expliquée en fonction du nombre de dimensions (simplement tracer cumsum ; voir figure ci-dessous). Il y aura généralement un coude dans la courbe, où la variance expliquée cesse de croître rapidement. Vous pouvez considérer cela comme la dimensionnalité intrinsèque de l’ensemble de données. Dans ce cas, vous pouvez voir que la réduction de la dimensionnalité à environ 100 dimensions ne perdrait pas trop de la variance expliquée.
from sklearn.datasets import load_digits
digits = load_digits()
pca = PCA().fit(digits.data)
plt.plot(np.cumsum(pca.explained_variance_ratio_))
plt.xlabel('Nombre de composante')
plt.ylabel('cumulative explained variance');
plt.show()
Réduction de la dimensionnalité par l’ACP¶
L’utilisation de l’ACP pour la réduction de la dimensionnalité implique la mise à zéro d’une ou de plusieurs des plus petites composantes principales, ce qui donne une projection à plus faible dimension des données qui préserve la variance maximale des données.
Voici un exemple d’utilisation de l’ACP comme transformation de réduction de la dimensionnalité :
pca = PCA(n_components=1)
pca.fit(X)
X_pca = pca.transform(X)
print("original shape: ", X.shape)
print("transformed shape:", X_pca.shape)
original shape: (60, 3)
transformed shape: (60, 1)
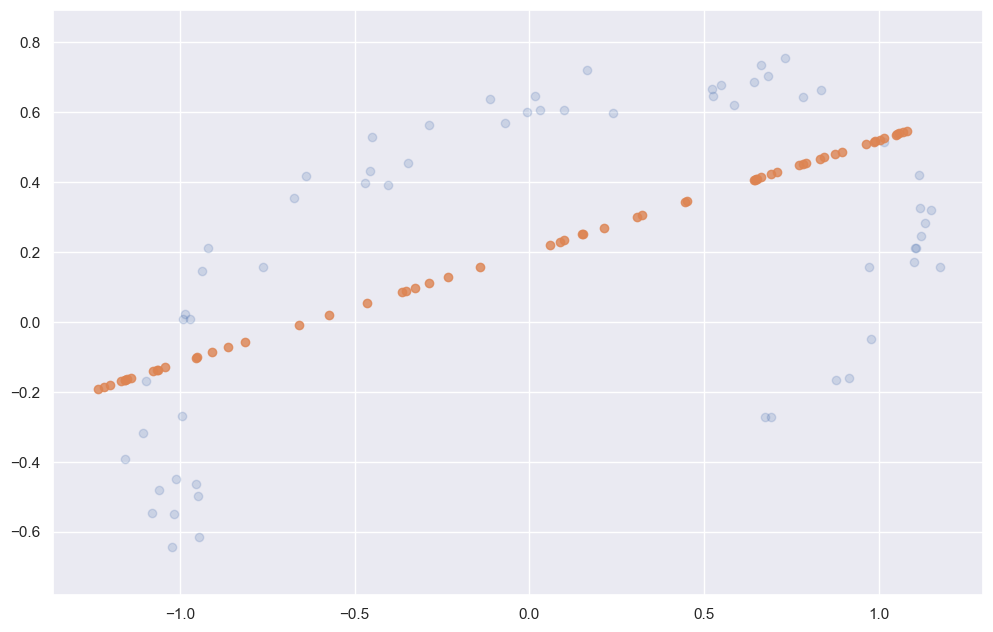
Les données transformées ont été réduites à une seule dimension. Pour comprendre l’effet de cette réduction de dimensionnalité, nous pouvons effectuer la transformation inverse de ces données réduites et la tracer avec les données originales :
fig = plt.figure(figsize=(12, 7.6))
X_new = pca.inverse_transform(X_pca)
plt.scatter(X[:, 0], X[:, 1], alpha=0.2)
plt.scatter(X_new[:, 0], X_new[:, 1], alpha=0.8)
plt.axis('equal');
plt.show()