K plus proches voisins (kNN)#
Note importante:#
Dans ce cours, nous adoptons une approche délibérément pratique de l’algorithme kNN. Notre objectif principal n’est pas d’explorer en profondeur la théorie mathématique sous-jacente, mais plutôt de développer des compétences pratiques.
Ce qui est attendu :#
Savoir interpréter chaque ligne de code et sa fonction
Être capable d’adapter le code à différentes situations pratiques
Maîtriser la préparation des données
Ce qui n’est pas attendu :#
La démonstration mathématique de l’algorithme
Les détails théoriques avancés du fonctionnement interne
L’optimisation algorithmique
Les cas d’usage complexes
Focus du cours :#
Compréhension du code : Que fait chaque ligne ?
Utilisation concrète : Comment l’appliquer à des cas réels ?
Concentrez-vous sur la compréhension pratique et l’application concrète.
Les codes que nous allons voir ensemble seront expliqués ligne par ligne. Ne vous inquiétez pas si la théorie sous-jacente semble complexe - concentrez-vous sur la compréhension pratique du code et son application.
Introduction#
L’algorithme des k plus proches voisins (kNN) est une méthode fondamentale en apprentissage automatique, particulièrement utile pour l’analyse statistique dans diverses applications comme :
La classification des risques en assurance
L’évaluation de la probabilité de réclamation
La segmentation des clients
Dans ce chapitre, nous allons utiliser kNN pour prédire si un assuré va renouveler son contrat d’assurance-vie en fonction de diverses caractéristiques.
1. Configuration de l’environnement#
Commençons par charger les bibliothèques nécessaires :
library(tidyverse) # Pour la manipulation et visualisation des données
library(class) # Pour l'algorithme kNN
library(caret) # Pour l'évaluation du modèle
library(scales) # Pour le formatage des échelles
# Définition d'une graine aléatoire pour la reproductibilité
set.seed(123)
── Attaching core tidyverse packages ────────
✔ dplyr 1.1.4 ✔ readr 2.1.5
✔ forcats 1.0.0 ✔ stringr 1.5.1
✔ ggplot2 3.5.1 ✔ tibble 3.2.1
✔ lubridate 1.9.3 ✔ tidyr 1.3.1
✔ purrr 1.0.2
── Conflicts ─────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
Loading required package: lattice
Attaching package: ‘caret’
The following object is masked from ‘package:purrr’:
lift
Attaching package: ‘scales’
The following object is masked from ‘package:purrr’:
discard
The following object is masked from ‘package:readr’:
col_factor
2. Génération des données#
Pour cet exemple, nous allons créer un jeu de données synthétiques qui simule des caractéristiques de clients d’assurance-vie.
n <- 1000 # nombre de clients
donnees <- tibble(
age = runif(n, 25, 75),
prime_annuelle = rlnorm(n, log(5000), 0.5),
anciennete = rpois(n, 5),
nb_reclamations = rpois(n, 0.5),
valeur_contrat = rlnorm(n, log(100000), 0.7)
)
# Création de la variable cible (renouvellement)
donnees <- donnees %>%
mutate(
prob_renouvellement = 1 / (1 + exp(-(
-2 +
0.03 * (age - 50) +
0.0001 * (prime_annuelle - 5000) +
0.2 * anciennete +
-0.5 * nb_reclamations +
0.00001 * (valeur_contrat - 100000)
))),
renouvellement = rbinom(n, 1, prob_renouvellement)
) %>%
select(-prob_renouvellement)
# Affichage des premières lignes
head(donnees)
| age | prime_annuelle | anciennete | nb_reclamations | valeur_contrat | renouvellement |
|---|---|---|---|---|---|
| <dbl> | <dbl> | <int> | <int> | <dbl> | <int> |
| 39.37888 | 3700.587 | 3 | 0 | 62178.22 | 1 |
| 64.41526 | 3042.223 | 9 | 1 | 149483.96 | 0 |
| 45.44885 | 8354.752 | 4 | 0 | 61069.34 | 0 |
| 69.15087 | 7278.819 | 6 | 1 | 68812.22 | 1 |
| 72.02336 | 2351.033 | 3 | 0 | 171956.13 | 0 |
| 27.27782 | 4767.701 | 6 | 0 | 71681.68 | 0 |
Explication des variables :
age: Âge du client (25-75 ans)prime_annuelle: Prime annuelle payée par le clientanciennete: Nombre d’années depuis la souscription initialenb_reclamations: Nombre de réclamations dans l’année précédentevaleur_contrat: Valeur totale du contratrenouvellement: Variable cible (1 = renouvelle, 0 = ne renouvelle pas)
3. Analyse exploratoire des données#
Avant d’appliquer kNN, explorons nos données pour mieux comprendre les relations entre les variables.
summary(donnees)
age prime_annuelle anciennete nb_reclamations
Min. :25.02 Min. : 1227 Min. : 0.00 Min. :0.000
1st Qu.:37.68 1st Qu.: 3544 1st Qu.: 3.00 1st Qu.:0.000
Median :49.50 Median : 5073 Median : 5.00 Median :0.000
Mean :49.86 Mean : 5707 Mean : 5.03 Mean :0.469
3rd Qu.:62.34 3rd Qu.: 6938 3rd Qu.: 7.00 3rd Qu.:1.000
Max. :74.97 Max. :27238 Max. :14.00 Max. :5.000
valeur_contrat renouvellement
Min. : 11188 Min. :0.000
1st Qu.: 63906 1st Qu.:0.000
Median : 97291 Median :0.000
Mean : 127887 Mean :0.317
3rd Qu.: 160478 3rd Qu.:1.000
Max. :1096563 Max. :1.000
# Visualisation de la distribution des variables numériques par statut de renouvellement
plot_distribution <- function(data, var, titre) {
ggplot(data, aes(x = !!sym(var), fill = factor(renouvellement))) +
geom_density(alpha = 0.5) +
labs(title = titre,
x = var,
y = "Densité",
fill = "Renouvellement") +
theme_minimal()
}
# Création des graphiques
p1 <- plot_distribution(donnees, "age", "Distribution de l'âge")
p2 <- plot_distribution(donnees, "prime_annuelle", "Distribution des primes annuelles")
p3 <- plot_distribution(donnees, "anciennete", "Distribution de l'ancienneté")
# Affichage des graphiques
gridExtra::grid.arrange(p1, p2, p3, ncol = 2)
Error in loadNamespace(x): there is no package called ‘gridExtra’
Traceback:
1. withRestarts(stop(cond), retry_loadNamespace = function() NULL)
2. withOneRestart(expr, restarts[[1L]])
3. doWithOneRestart(return(expr), restart)
4. stop(cond)
Explication : L’analyse exploratoire nous permet de :
Identifier les différences de distribution entre les clients qui renouvellent et ceux qui ne renouvellent pas
Détecter d’éventuelles valeurs aberrantes
Comprendre les relations entre les variables
4. Prétraitement des données#
kNN est sensible à l’échelle des variables. Nous devons donc normaliser nos données.
# Fonction de normalisation
normaliser <- function(x) {
return((x - min(x)) / (max(x) - min(x)))
}
# Application de la normalisation
donnees_norm <- donnees %>%
mutate(across(-renouvellement, normaliser))
# Division en ensembles d'entraînement et de test
indices_train <- createDataPartition(donnees_norm$renouvellement, p = 0.8, list = FALSE)
train_data <- donnees_norm[indices_train, ]
test_data <- donnees_norm[-indices_train, ]
# Séparation des caractéristiques et de la variable cible
X_train <- train_data %>% select(-renouvellement) %>% as.matrix()
y_train <- train_data$renouvellement
X_test <- test_data %>% select(-renouvellement) %>% as.matrix()
y_test <- test_data$renouvellement
Explication :
La normalisation met toutes les variables à la même échelle [0,1]
Nous utilisons 80% des données pour l’entraînement et 20% pour le test
Les données sont converties en matrices pour l’algorithme kNN
5. Application de l’algorithme kNN#
Maintenant, appliquons l’algorithme kNN avec différentes valeurs de k pour trouver la meilleure configuration.
# Test de différentes valeurs de k
k_values <- seq(1, 30, by = 2)
accuracy <- numeric(length(k_values))
for(i in seq_along(k_values)) {
predictions <- knn(train = X_train,
test = X_test,
cl = factor(y_train),
k = k_values[i])
cm <- confusionMatrix(predictions, factor(y_test))
accuracy[i] <- cm$overall["Accuracy"]
}
# Visualisation des résultats
resultats_k <- tibble(k = k_values, accuracy = accuracy)
ggplot(resultats_k, aes(x = k, y = accuracy)) +
geom_line() +
geom_point() +
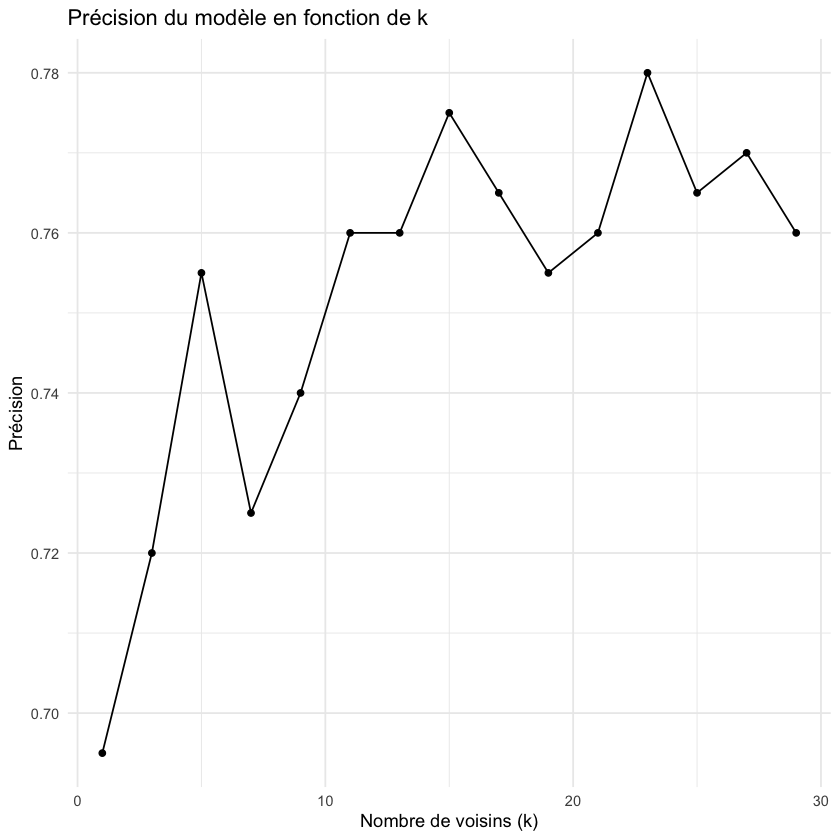
labs(title = "Précision du modèle en fonction de k",
x = "Nombre de voisins (k)",
y = "Précision") +
theme_minimal()
# Sélection du meilleur k
k_optimal <- k_values[which.max(accuracy)]
print(paste("Valeur optimale de k:", k_optimal))
Explication :
Nous testons différentes valeurs de k pour trouver celle qui donne les meilleures performances
Un k trop petit peut conduire à du surapprentissage
Un k trop grand peut perdre des patterns importants dans les données
6. Évaluation du modèle#
Évaluons les performances du modèle avec la valeur optimale de k.
# Prédictions finales avec le k optimal
predictions_finales <- knn(train = X_train,
test = X_test,
cl = factor(y_train),
k = k_optimal)
# Matrice de confusion
cm_final <- confusionMatrix(predictions_finales, factor(y_test))
print(cm_final)
# Calcul des métriques importantes pour l'actuariat
metriques <- data.frame(
Métrique = c("Précision", "Sensibilité", "Spécificité", "Valeur Prédictive Positive"),
Valeur = c(
cm_final$overall["Accuracy"],
cm_final$byClass["Sensitivity"],
cm_final$byClass["Specificity"],
cm_final$byClass["Pos Pred Value"]
)
)
print(metriques)
Confusion Matrix and Statistics
Reference
Prediction 0 1
0 139 42
1 2 17
Accuracy : 0.78
95% CI : (0.7161, 0.8354)
No Information Rate : 0.705
P-Value [Acc > NIR] : 0.01075
Kappa : 0.3412
Mcnemar's Test P-Value : 4.116e-09
Sensitivity : 0.9858
Specificity : 0.2881
Pos Pred Value : 0.7680
Neg Pred Value : 0.8947
Prevalence : 0.7050
Detection Rate : 0.6950
Detection Prevalence : 0.9050
Balanced Accuracy : 0.6370
'Positive' Class : 0
Métrique Valeur
Accuracy Précision 0.7800000
Sensitivity Sensibilité 0.9858156
Specificity Spécificité 0.2881356
Pos Pred Value Valeur Prédictive Positive 0.7679558
Explication des métriques :
Précision : Proportion totale de prédictions correctes
Sensibilité : Capacité à identifier les vrais renouvellements
Spécificité : Capacité à identifier les non-renouvellements
Valeur Prédictive Positive : Probabilité qu’un client prédit comme renouvelant renouvelle effectivement
7. Application pratique#
Utilisons notre modèle pour prédire le renouvellement pour de nouveaux clients.
# Fonction de prédiction pour un nouveau client
predire_renouvellement <- function(age, prime, anciennete, reclamations, valeur) {
# Création du nouveau cas
nouveau_client <- data.frame(
age = age,
prime_annuelle = prime,
anciennete = anciennete,
nb_reclamations = reclamations,
valeur_contrat = valeur
)
# Normalisation des données du nouveau client
nouveau_client_norm <- as.matrix(mapply(function(x, col) {
(x - min(donnees[[col]])) / (max(donnees[[col]]) - min(donnees[[col]]))
}, nouveau_client, names(nouveau_client)))
# Prédiction
prediction <- knn(train = X_train,
test = nouveau_client_norm,
cl = factor(y_train),
k = k_optimal)
return(prediction)
}
# Exemple d'utilisation
nouveau_client <- predire_renouvellement(
age = 45,
prime = 6000,
anciennete = 3,
reclamations = 0,
valeur = 120000
)
print(paste("Prédiction pour le nouveau client:",
ifelse(nouveau_client == 1, "Va renouveler", "Ne va pas renouveler")))
Error in knn(train = X_train, test = nouveau_client_norm, cl = factor(y_train), : dims of 'test' and 'train' differ
Traceback:
1. predire_renouvellement(age = 45, prime = 6000, anciennete = 3,
. reclamations = 0, valeur = 120000)
2. knn(train = X_train, test = nouveau_client_norm, cl = factor(y_train),
. k = k_optimal) # at line 18-21 of file <text>
3. stop("dims of 'test' and 'train' differ")
Conclusion#
Dans ce cours, nous avons :
Préparé et exploré des données d’assurance-vie
Appliqué l’algorithme kNN pour prédire les renouvellements
Évalué les performances du modèle
Créé une fonction pratique pour prédire de nouveaux cas
Points importants pour les actuaires :
kNN est simple mais efficace pour la classification
La normalisation des données est cruciale
Le choix de k impacte significativement les performances
L’interprétation des résultats doit tenir compte du contexte métier
Exercices suggérés#
Modifiez le code pour tester d’autres méthodes de normalisation
Ajoutez de nouvelles variables pertinentes pour l’assurance-vie
Comparez les performances de kNN avec d’autres algorithmes (ex: régression logistique)\
Très optionels#
Analysez l’impact de différentes métriques de distance
Créez une visualisation des k plus proches voisins pour un cas spécifique