Application: Classification transaction bancaire#
Introduction#
Dans ce tutoriel, nous allons explorer un exemple concret de classification binaire dans le domaine financier. Un exemple de la détection de fraude par carte de crédit. Nous utiliserons la régression logistique, pour prédire si une transaction est frauduleuse ou non.
Commençons par charger les bibliothèques nécessaires :
library(tidyverse) # Pour la manipulation et visualisation des données
library(caret) # Pour la préparation des données et l'évaluation du modèle
library(pROC) # Pour la courbe ROC
set.seed(3035)
── Attaching core tidyverse packages ────────
✔ dplyr 1.1.4 ✔ readr 2.1.5
✔ forcats 1.0.0 ✔ stringr 1.5.1
✔ ggplot2 3.5.1 ✔ tibble 3.2.1
✔ lubridate 1.9.3 ✔ tidyr 1.3.1
✔ purrr 1.0.2
── Conflicts ─────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
Loading required package: lattice
Attaching package: ‘caret’
The following object is masked from ‘package:purrr’:
lift
Type 'citation("pROC")' for a citation.
Attaching package: ‘pROC’
The following objects are masked from ‘package:stats’:
cov, smooth, var
1. Génération de données synthétiques#
Dans un cas réel, nous utiliserions des données historiques de transactions. Pour ce tutoriel, nous allons générer des données que nous créons qui simulent des transactions par carte de crédit.
generer_normales <- function(n) {
tibble(
montant = rlnorm(n, meanlog = 4, sdlog = 1),
heure = sample(0:23, n, replace = TRUE),
jour_semaine = sample(1:7, n, replace = TRUE),
age_compte = runif(n, 0, 3650),
fraude = 0
)
}
generer_frauduleuses <- function(n) {
tibble(
montant = rlnorm(n, meanlog = 5, sdlog = 1.5),
heure = sample(0:23, n, replace = TRUE, prob = c(rep(1, 6), rep(3, 18))),
jour_semaine = sample(1:7, n, replace = TRUE),
age_compte = runif(n, 0, 365),
fraude = 1
)
}
n <- 10000 # nombre total de transactions
donnees_normales <- generer_normales(n * 0.99) # 99% de transactions normales
donnees_frauduleuses <- generer_frauduleuses(n * 0.01) # 1% de transactions frauduleuses
donnees <- bind_rows(donnees_normales, donnees_frauduleuses)
head(donnees)
| montant | heure | jour_semaine | age_compte | fraude |
|---|---|---|---|---|
| <dbl> | <int> | <int> | <dbl> | <dbl> |
| 24.45815 | 1 | 6 | 2375.5742 | 0 |
| 74.17737 | 18 | 7 | 1326.5493 | 0 |
| 51.12859 | 12 | 7 | 1245.7210 | 0 |
| 220.46457 | 4 | 4 | 77.3116 | 0 |
| 113.68081 | 1 | 7 | 1917.0361 | 0 |
| 18.25704 | 18 | 3 | 3307.5299 | 0 |
Show code cell source
write.csv(donnees, "fraud_Cc.csv", row.names=F)
2. Exploration des données#
Show code cell source
summary(donnees)
montant heure jour_semaine age_compte
Min. : 1.376 Min. : 0.00 Min. :1.000 Min. : 0.138
1st Qu.: 28.026 1st Qu.: 5.00 1st Qu.:2.000 1st Qu.: 919.926
Median : 56.426 Median :11.00 Median :4.000 Median :1833.957
Mean : 93.171 Mean :11.46 Mean :3.991 Mean :1823.207
3rd Qu.: 109.311 3rd Qu.:17.00 3rd Qu.:6.000 3rd Qu.:2744.068
Max. :2428.218 Max. :23.00 Max. :7.000 Max. :3648.681
fraude
Min. :0.00
1st Qu.:0.00
Median :0.00
Mean :0.01
3rd Qu.:0.00
Max. :1.00
Show code cell source
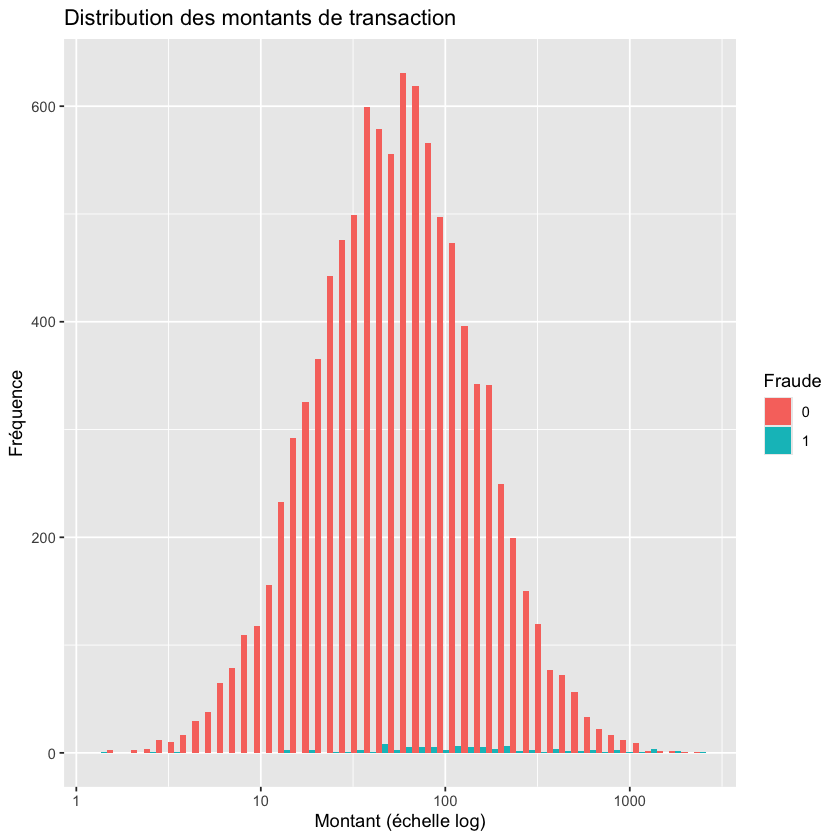
ggplot(donnees, aes(x = montant, fill = factor(fraude))) +
geom_histogram(bins = 50, position = "dodge") +
scale_x_log10() +
labs(title = "Distribution des montants de transaction",
x = "Montant (échelle log)", y = "Fréquence", fill = "Fraude")
Show code cell source
ggplot(donnees, aes(x = factor(heure), fill = factor(fraude))) +
geom_bar(position = "fill") +
labs(title = "Proportion de fraudes par heure",
x = "Heure", y = "Proportion", fill = "Fraude")
3. Prétraitement des données#
Préparons nos données pour la modélisation :
Show code cell source
# Conversion de 'fraude' en facteur afin de rendre ces variable catégorielles
donnees$fraude <- as.factor(donnees$fraude)
Show code cell source
# Normalisation des variables numériques
preprocess_params <- preProcess(donnees %>% select(-fraude), method = c("center", "scale"))
donnees_normalisees <- predict(preprocess_params, donnees)
Show code cell source
# Division en ensembles d'entraînement et de test
indices_partition <- createDataPartition(donnees_normalisees$fraude, p = 0.8, list = FALSE)
donnees_train <- donnees_normalisees[indices_partition, ]
donnees_test <- donnees_normalisees[-indices_partition, ]
Show code cell source
write.csv(donnees_train, "donnees_train_Cc.csv", row.names=F)
write.csv(donnees_test, "donnees_test_Cc.csv", row.names=F)
Show code cell source
print(paste("Dimensions de l'ensemble d'entraînement :", paste(dim(donnees_train), collapse = " x ")))
print(paste("Dimensions de l'ensemble de test :", paste(dim(donnees_test), collapse = " x ")))
[1] "Dimensions de l'ensemble d'entraînement : 8000 x 5"
[1] "Dimensions de l'ensemble de test : 2000 x 5"
4. Construction du modèle de régression logistique#
Show code cell source
modele_log <- glm(fraude ~ ., data = donnees_train, family = binomial())
summary(modele_log)
Call:
glm(formula = fraude ~ ., family = binomial(), data = donnees_train)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -10.71128 0.93335 -11.476 < 2e-16 ***
montant 0.46174 0.06210 7.435 1.04e-13 ***
heure 0.37870 0.13171 2.875 0.00404 **
jour_semaine -0.08803 0.12449 -0.707 0.47948
age_compte -5.08255 0.60575 -8.390 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 896.02 on 7999 degrees of freedom
Residual deviance: 536.62 on 7995 degrees of freedom
AIC: 546.62
Number of Fisher Scoring iterations: 11
5. Évaluation du modèle#
Évaluons la performance de notre modèle :
predictions_prob <- predict(modele_log, newdata = donnees_test, type = "response")
predictions_classe <- ifelse(predictions_prob > 0.5, 1, 0)
# Matrice de confusion
matrice_confusion <- confusionMatrix(factor(predictions_classe), donnees_test$fraude)
print(matrice_confusion)
Confusion Matrix and Statistics
Reference
Prediction 0 1
0 1979 17
1 1 3
Accuracy : 0.991
95% CI : (0.9858, 0.9947)
No Information Rate : 0.99
P-Value [Acc > NIR] : 0.380573
Kappa : 0.2475
Mcnemar's Test P-Value : 0.000407
Sensitivity : 0.9995
Specificity : 0.1500
Pos Pred Value : 0.9915
Neg Pred Value : 0.7500
Prevalence : 0.9900
Detection Rate : 0.9895
Detection Prevalence : 0.9980
Balanced Accuracy : 0.5747
'Positive' Class : 0
# Courbe ROC
courbe_roc <- roc(donnees_test$fraude, predictions_prob)
plot(courbe_roc, main = "Courbe ROC pour la détection de fraude")
print(paste("AUC :", auc(courbe_roc)))
Setting levels: control = 0, case = 1
Setting direction: controls < cases
[1] "AUC : 0.968156565656562"
6. Prédiction sur de nouvelles données#
Utilisons notre modèle pour prédire la probabilité de fraude pour une nouvelle transaction :
nouvelle_transaction <- tibble(
montant = 1000,
heure = 14,
jour_semaine = 3,
age_compte = 730
)
# Normalisation de la nouvelle transaction
nouvelle_transaction_norm <- predict(preprocess_params, nouvelle_transaction)
# Prédiction
proba_fraude <- predict(modele_log, nouvelle_transaction_norm, type = "response")
print(paste("Probabilité de fraude pour la nouvelle transaction :", round(proba_fraude, 4)))
[1] "Probabilité de fraude pour la nouvelle transaction : 0.1224"
Conclusion#
Dans ce tutoriel, nous avons construit un modèle de régression logistique pour détecter les fraudes par carte de crédit. Voici les points clés à retenir :
La préparation et l’exploration des données sont cruciales avant la modélisation.
La régression logistique est un outil puissant pour la classification binaire.
L’évaluation du modèle implique plusieurs métriques, dont la matrice de confusion et la courbe ROC.
L’interprétation des coefficients nous donne des insights sur l’importance des variables.
Le modèle peut être utilisé pour prédire la probabilité de fraude sur de nouvelles transactions.
Dans un contexte réel, ce modèle pourrait être utilisé comme un système d’alerte précoce, identifiant les transactions à haut risque pour une vérification plus approfondie.
Exercices#
Ces exercices sont conçus pour renforcer votre compréhension de la classification binaire en utilisant R, en s’appuyant sur l’exemple de détection de fraude par carte de crédit.
Exercice 1 : Exploration et visualisation des données#
Objectif : Approfondir l’analyse exploratoire des données.
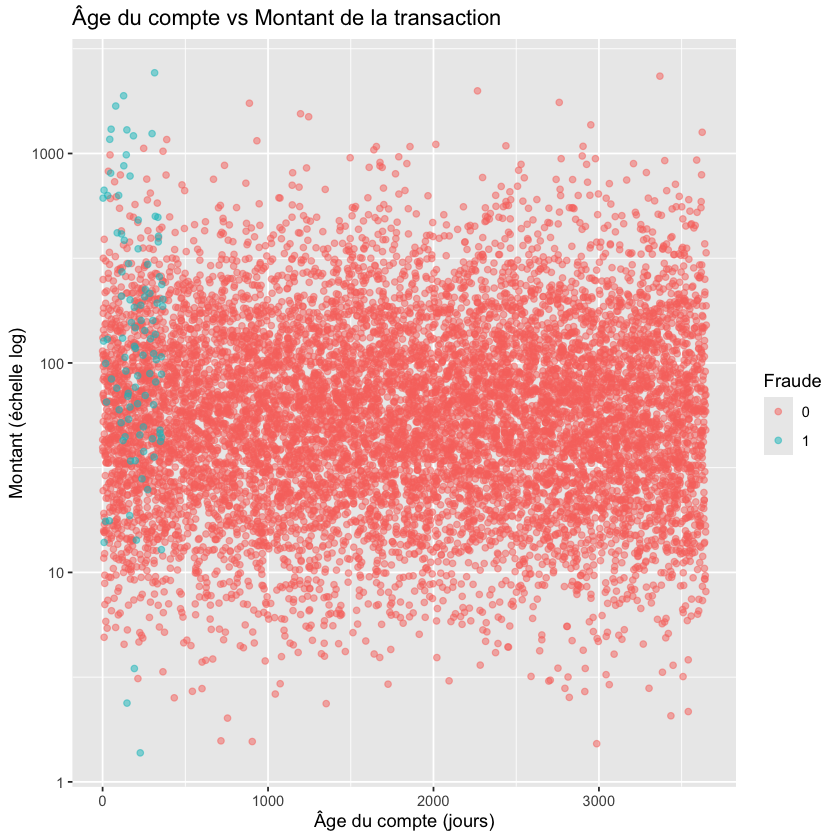
a) Créez un graphique montrant la relation entre l’âge du compte et le montant de la transaction, coloré par le statut de fraude.
b) Calculez et affichez le pourcentage de transactions frauduleuses par jour de la semaine. Quel jour semble avoir le plus haut taux de fraude ?
Show code cell source
ggplot(donnees, aes(x = age_compte, y = montant, color = factor(fraude))) +
geom_point(alpha = 0.5) +
scale_y_log10() +
labs(title = "Âge du compte vs Montant de la transaction",
x = "Âge du compte (jours)", y = "Montant (échelle log)", color = "Fraude")
Show code cell source
donnees %>%
group_by(jour_semaine) %>%
summarise(taux_fraude = mean(fraude == 1) * 100) %>%
arrange(desc(taux_fraude))
| jour_semaine | taux_fraude |
|---|---|
| <int> | <dbl> |
| 2 | 1.4634146 |
| 1 | 1.1821975 |
| 6 | 1.0416667 |
| 7 | 0.9859155 |
| 4 | 0.9372747 |
| 3 | 0.8191126 |
| 5 | 0.5653710 |
Exercice 2 : Prétraitement des données#
Objectif : Expérimenter avec différentes techniques de prétraitement.
a) Au lieu de normaliser les variables numériques, essayez de les standardiser (z-score). Comment cela affecte-t-il les résultats du modèle ?
b) Créez une nouvelle variable catégorielle “periode_jour” basée sur l’heure (matin : 6-12, après-midi : 12-18, soir : 18-24, nuit : 0-6). Incluez cette nouvelle variable dans le modèle.
Show code cell source
# Standardisation
preprocess_params <- preProcess(donnees %>% select(-fraude), method = c("center", "scale"))
donnees_standardisees <- predict(preprocess_params, donnees)
Show code cell source
# Création de la variable 'periode_jour'
donnees <- donnees %>%
mutate(periode_jour = case_when(
heure >= 6 & heure < 12 ~ "matin",
heure >= 12 & heure < 18 ~ "après-midi",
heure >= 18 & heure < 24 ~ "soir",
TRUE ~ "nuit"
))
Exercice 3 : Gestion du déséquilibre des classes#
Objectif : Comprendre l’impact du déséquilibre des classes sur le modèle.
a) Utilisez la technique de sous-échantillonnage pour équilibrer les classes dans l’ensemble d’entraînement. Comment cela affecte-t-il les performances du modèle ?
b) Expérimentez avec différents seuils de classification (au lieu de 0.5). Comment cela affecte-t-il la précision et le rappel du modèle ?
Show code cell source
donnees_equilibrees <- downSample(x = donnees_train[, -which(names(donnees_train) == "fraude")],
y = donnees_train$fraude)
Show code cell source
# Différents seuils
seuils <- seq(0.1, 0.9, by = 0.1)
resultats <- data.frame()
for (seuil in seuils) {
predictions_classe <- ifelse(predictions_prob > seuil, 1, 0)
cm <- confusionMatrix(factor(predictions_classe), donnees_test$fraude)
resultats <- rbind(resultats, data.frame(Seuil = seuil,
Precision = cm$byClass["Precision"],
Rappel = cm$byClass["Recall"]))
}
print(resultats)
Seuil Precision Rappel
Precision 0.1 0.9933368 0.9787879
Precision1 0.2 0.9924661 0.9979798
Precision2 0.3 0.9924699 0.9984848
Precision3 0.4 0.9924774 0.9994949
Precision4 0.5 0.9914830 0.9994949
Precision5 0.6 0.9914872 1.0000000
Precision6 0.7 0.9909910 1.0000000
Precision7 0.8 0.9909910 1.0000000
Precision8 0.9 0.9909910 1.0000000