Application: retards d’avions#
Problème : Prédire les retards d’arrivée des vols
À propos des données#
Dans cet exemple sur les compagnies aériennes, l’ensemble de données flight_delay est généré de manière synthétique et est utilisé pour développer le modèle de régression linéaire multiple afin de prédire les retards d’arrivée des vols.
L’ensemble de données contient au total 3 593 observations et 11 variables ; 10 variables sont numériques et 1 variable est catégorique. Arr_Delay est la variable dépendante ou variable cible qui est continue dans la nature et toutes les autres variables sont indépendantes ou variables explicatives dans les données.
Lire les données à partir du répertoire de travail, créez votre propre répertoire de travail directement pour lire l’ensemble de données.
Show code cell source
data1 <- read.csv("flight_delay.csv", header=TRUE, sep=",")
Afficher les 6 premières lignes de l’ensemble de données pour voir à quoi ressemblent les données
Show code cell source
head(data1)
| Carrier | Airport_Distance | Number_of_flights | Weather | Support_Crew_Available | Baggage_loading_time | Late_Arrival_o | Cleaning_o | Fueling_o | Security_o | Arr_Delay | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| <chr> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | |
| 1 | UA | 437 | 41300 | 5 | 83 | 17 | 19 | 15 | 26 | 31 | 58 |
| 2 | UA | 451 | 41516 | 5 | 82 | 17 | 19 | 15 | 22 | 32 | 48 |
| 3 | AA | 425 | 37404 | 5 | 175 | 16 | 17 | 14 | 28 | 29 | 16 |
| 4 | B6 | 454 | 44798 | 6 | 49 | 18 | 19 | 13 | 29 | 31 | 81 |
| 5 | DL | 455 | 40643 | 6 | 55 | 17 | 19 | 18 | 26 | 37 | 62 |
| 6 | UA | 416 | 39707 | 5 | 146 | 16 | 19 | 6 | 28 | 31 | 34 |
Décrire la structure des données#
Show code cell source
str(data1)
'data.frame': 3593 obs. of 11 variables:
$ Carrier : chr "UA" "UA" "AA" "B6" ...
$ Airport_Distance : int 437 451 425 454 455 416 439 446 441 456 ...
$ Number_of_flights : int 41300 41516 37404 44798 40643 39707 45627 40415 42248 43453 ...
$ Weather : int 5 5 5 6 6 5 5 5 6 6 ...
$ Support_Crew_Available: int 83 82 175 49 55 146 141 145 58 3 ...
$ Baggage_loading_time : int 17 17 16 18 17 16 16 17 17 18 ...
$ Late_Arrival_o : int 19 19 17 19 19 19 19 18 19 19 ...
$ Cleaning_o : int 15 15 14 13 18 6 15 9 9 10 ...
$ Fueling_o : int 26 22 28 29 26 28 21 25 17 24 ...
$ Security_o : int 31 32 29 31 37 31 39 39 53 36 ...
$ Arr_Delay : int 58 48 16 81 62 34 63 47 39 122 ...
Nom de la colonne (variables)#
Afficher le nom de la colonne (variables) des données
Show code cell source
names(data1)
- 'Carrier'
- 'Airport_Distance'
- 'Number_of_flights'
- 'Weather'
- 'Support_Crew_Available'
- 'Baggage_loading_time'
- 'Late_Arrival_o'
- 'Cleaning_o'
- 'Fueling_o'
- 'Security_o'
- 'Arr_Delay'
Statistiques descriptives#
Afficher les statistiques descriptives des données
Show code cell source
summary(data1$Arr_Delay)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0 49.0 70.0 69.8 90.0 180.0
Valeurs manquantes#
Vérifions les valeurs manquantes présentes dans les données
Show code cell source
sum(is.na(data1))
Corrélation entre les variables#
Déterminer la corrélation entre les variables
Show code cell source
corr <- cor.test(data1$Arr_Delay,data1$Number_of_flights, method = "pearson" )
Show code cell source
corr
Pearson's product-moment correlation
data: data1$Arr_Delay and data1$Number_of_flights
t = 86.823, df = 3591, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.8121611 0.8332786
sample estimates:
cor
0.823004
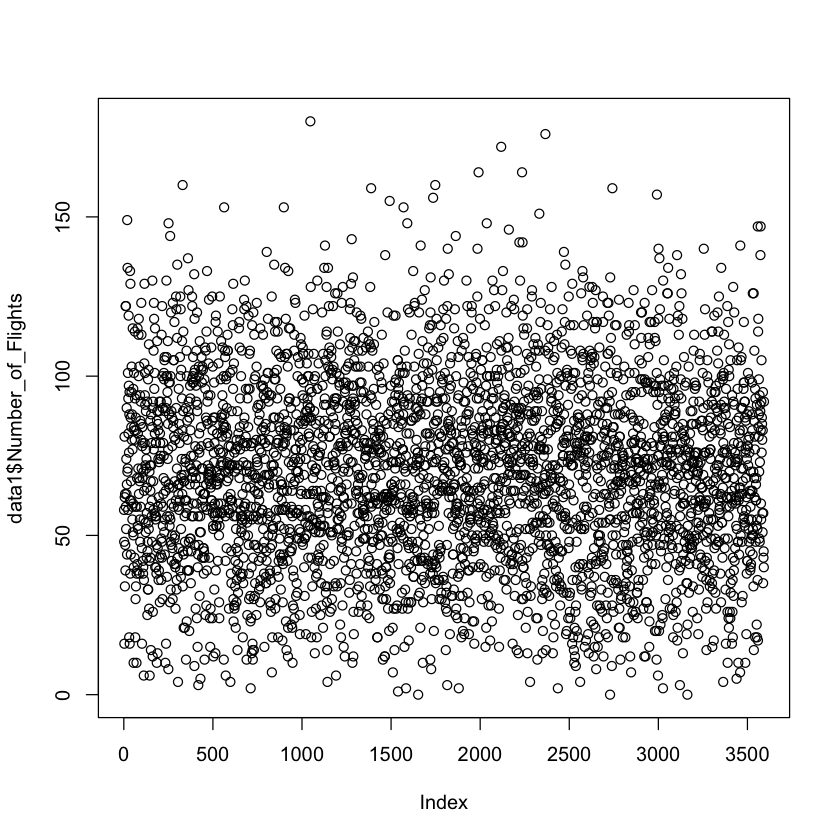
La méthode de corrélation des moments de Pearson est utilisée pour découvrir la corrélation entre deux variables. Il existe une forte corrélation positive (82 %) entre Arr_Delay et Number_of_Flights, ce qui signifie que les deux variables sont directement proportionnelles l’une à l’autre. Arr_Delay augmente avec l’augmentation de Number_of_Flights. Pour déterminer si la corrélation entre les variables est significative, nous devons comparer la valeur p avec le niveau de signification (0.05). Dans ce cas, la valeur p pour la corrélation entre Arr_Delay et Number_of_Flights est inférieure au niveau de signification de 0.05, ce qui indique que le coefficient de corrélation est significatif.
4 en 1#
Pour ajouter quatre graphiques dans une seule fenêtre ou un panneau de tracé
Show code cell source
par(mfrow = c(2, 2))
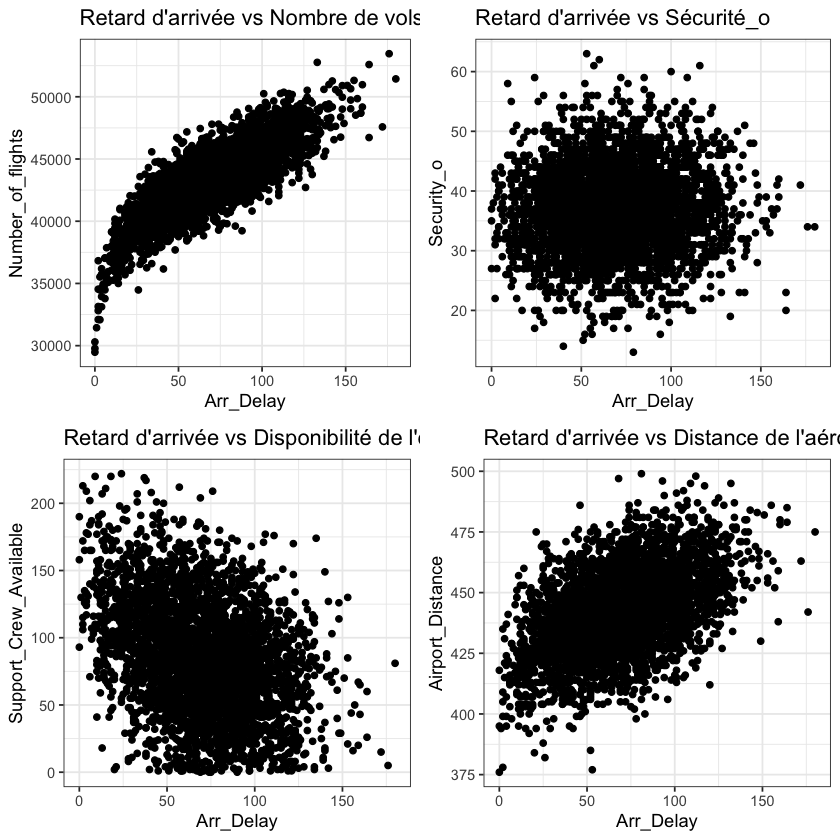
Quelques graphiques#
Pour tracer la variable dépendante et la variable indépendante
# install.packages("gridExtra")
Show code cell source
library(ggplot2)
library(gridExtra)
Error in library(gridExtra): there is no package called ‘gridExtra’
Traceback:
1. stop(packageNotFoundError(package, lib.loc, sys.call()))
Show code cell source
p1 <- ggplot(data1, aes(x = Arr_Delay, y = Number_of_flights)) +
geom_point() +
theme_bw() +
ggtitle("Retard d'arrivée vs Nombre de vols")
Show code cell source
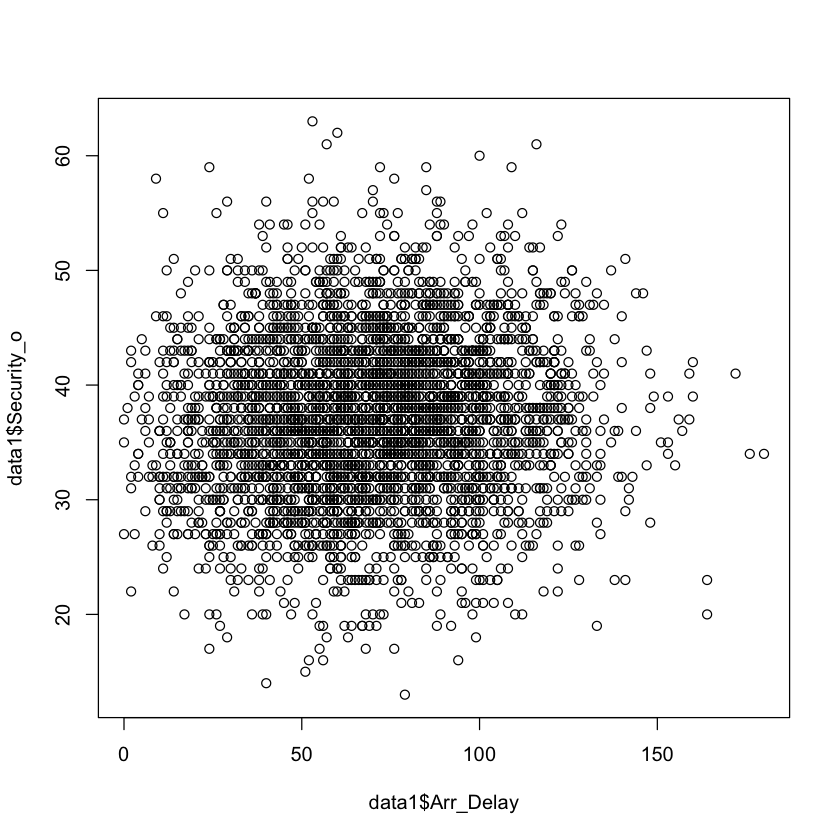
p2 <- ggplot(data1, aes(x = Arr_Delay, y = Security_o)) +
geom_point() +
theme_bw() +
ggtitle("Retard d'arrivée vs Sécurité_o")
Show code cell source
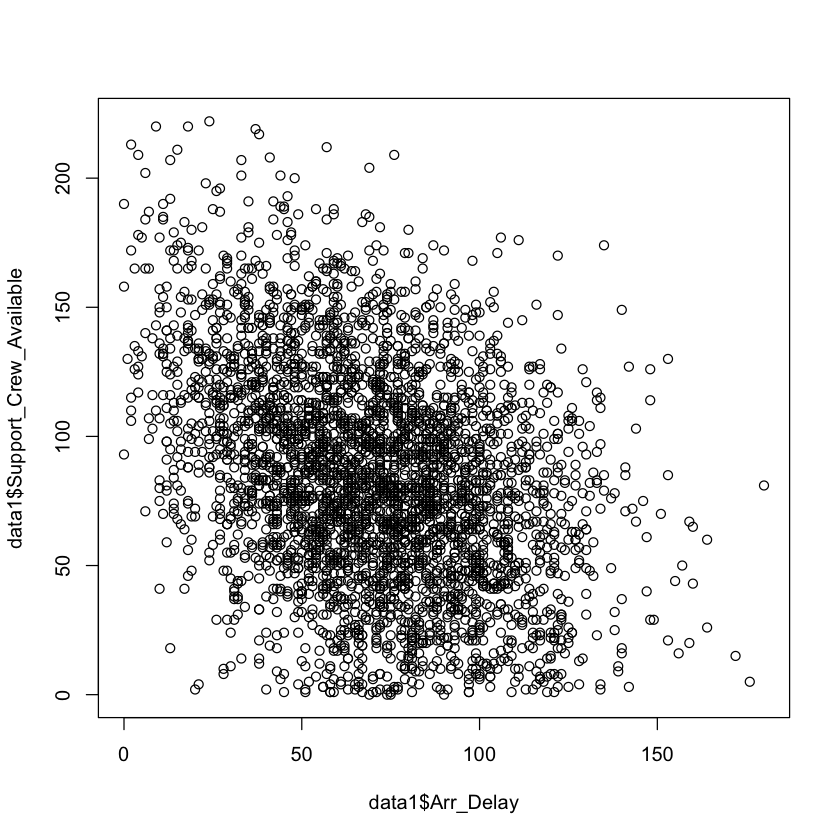
p3 <- ggplot(data1, aes(x = Arr_Delay, y = Support_Crew_Available)) +
geom_point() +
theme_bw() +
ggtitle("Retard d'arrivée vs Disponibilité de l'équipage de soutien")
Show code cell source
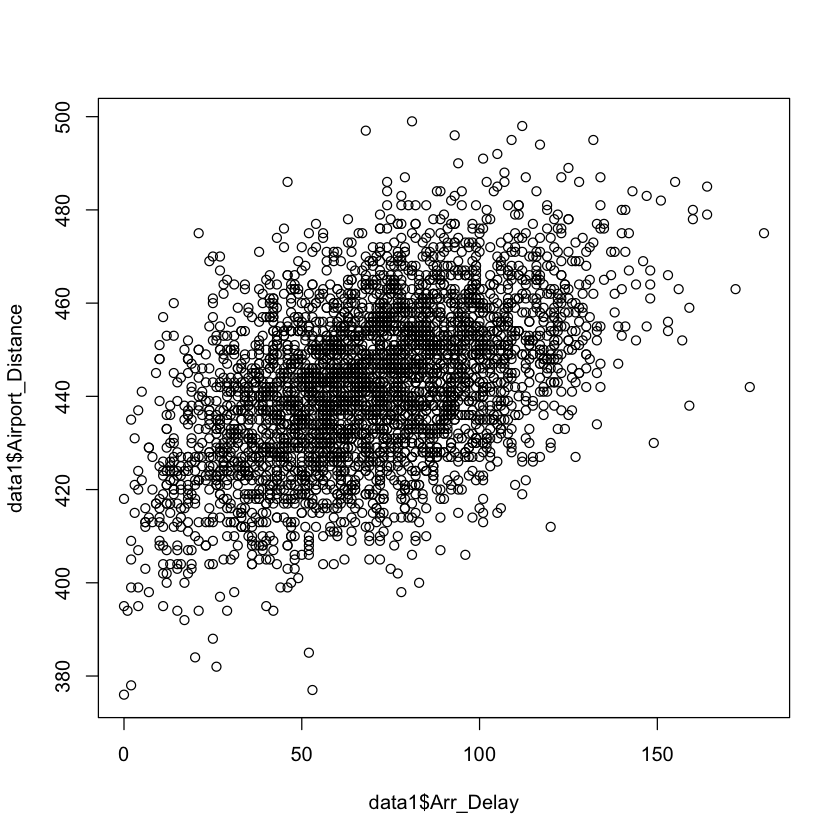
p4 <- ggplot(data1, aes(x = Arr_Delay, y = Airport_Distance)) +
geom_point() +
theme_bw() +
ggtitle("Retard d'arrivée vs Distance de l'aéroport")
# Utiliser grid.arrange pour arranger les graphiques
grid.arrange(p1, p2, p3, p4, ncol = 2, nrow = 2)
Pour supprimer la première variable (Carrier) de data1
Show code cell source
data2 <- data1[-c(1)]
Division de l’ensemble de données#
en un ensemble de données d”entrainement et un ensemble de données de test
Les données sont divisées en deux parties, l’ensemble de données de train et l’ensemble de données de test, au moyen d’un échantillonnage aléatoire stratifié, et le ratio de division est de 70:30, ce qui signifie que 70 % des données contribuent à l’ensemble de données de train et 30 % des données contribuent à l’ensemble de données de test.
L’ensemble de données de train est utilisé pour construire le modèle et l’ensemble de données de test est utilisé pour tester la performance du modèle.
Show code cell source
#Installation de caTools pour division des données
library(caTools)
set.seed(3035)
sample <- sample.split(data2$Arr_Delay,SplitRatio=0.70)
train_data <- subset(data2,sample==TRUE)
test_data <- subset(data2,sample==FALSE)
Updating HTML index of packages in '.Library'
Making 'packages.html' ...
done
L’ensemble de données Train_data est utilisé pour construire le modèle et l’ensemble de données Test_ est utilisé pour tester la performance du modèle. #Construction d’un modèle de régression linéaire multiple à l’aide de lm sur l’ensemble de données
Show code cell source
model <- lm(Arr_Delay ~., data = train_data)
summary(model)
Call:
lm(formula = Arr_Delay ~ ., data = train_data)
Residuals:
Min 1Q Median 3Q Max
-35.780 -8.151 -0.583 8.230 70.332
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -5.801e+02 8.943e+00 -64.861 < 2e-16 ***
Airport_Distance 1.751e-01 1.613e-02 10.852 < 2e-16 ***
Number_of_flights 4.418e-03 1.281e-04 34.486 < 2e-16 ***
Weather 4.721e+00 5.403e-01 8.737 < 2e-16 ***
Support_Crew_Available -5.113e-02 6.398e-03 -7.991 2.03e-15 ***
Baggage_loading_time 1.353e+01 5.238e-01 25.835 < 2e-16 ***
Late_Arrival_o 6.999e+00 3.931e-01 17.804 < 2e-16 ***
Cleaning_o 1.176e-01 7.106e-02 1.654 0.0982 .
Fueling_o -1.016e-01 7.086e-02 -1.433 0.1519
Security_o 8.947e-03 3.505e-02 0.255 0.7985
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 12.38 on 2504 degrees of freedom
Multiple R-squared: 0.8213, Adjusted R-squared: 0.8206
F-statistic: 1279 on 9 and 2504 DF, p-value: < 2.2e-16
Dans le code ci-dessus, l’ajustement lm (modèle linéaire) est utilisée pour construire le modèle de régression linéaire multiple. Arr_Delay est la variable dépendante ou cible dans les données et toutes les autres variables sont des variables indépendantes ou explicatives.
L’ensemble de données Train_data est utilisé pour entraîner le modèle et le sommaire du modèle affiche le tableau des coefficients et les statistiques du modèle. La liste 6-1 affiche le tableau des coefficients et les statistiques du modèle.
En examinant les coefficients dans le résultat, on constate que certaines variables ont une valeur p inférieure à 0,001 et sont donc des variables significatives du modèle, mais que d’autres variables comme Cleaning_o, Fueling_o et Security_o ont une valeur p supérieure à 0,001 et ne sont donc pas des variables significatives du modèle. Supprimons toutes les variables non significatives du modèle et réexécutons le modèle.
Modèle final#
de régression linéaire multiple avec les variables significatives variables significatives sur l’ensemble de données train_data
Show code cell source
model_sig<-lm(Arr_Delay~Airport_Distance+Number_of_flights
+Weather+Support_Crew_Available+Baggage_loading_time
+Late_Arrival_o, data= train_data)
model_sig
summary(model_sig)
Call:
lm(formula = Arr_Delay ~ Airport_Distance + Number_of_flights +
Weather + Support_Crew_Available + Baggage_loading_time +
Late_Arrival_o, data = train_data)
Residuals:
Min 1Q Median 3Q Max
-36.224 -8.213 -0.677 8.295 70.468
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -5.809e+02 8.705e+00 -66.734 < 2e-16 ***
Airport_Distance 1.754e-01 1.613e-02 10.877 < 2e-16 ***
Number_of_flights 4.424e-03 1.280e-04 34.570 < 2e-16 ***
Weather 4.688e+00 5.400e-01 8.683 < 2e-16 ***
Support_Crew_Available -5.171e-02 6.394e-03 -8.087 9.38e-16 ***
Baggage_loading_time 1.350e+01 5.232e-01 25.804 < 2e-16 ***
Late_Arrival_o 7.007e+00 3.930e-01 17.828 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 12.39 on 2507 degrees of freedom
Multiple R-squared: 0.8209, Adjusted R-squared: 0.8205
F-statistic: 1916 on 6 and 2507 DF, p-value: < 2.2e-16
Analyse du modèle final#
Le code ci-dessus montre les coefficients (étiquetés Estimates), leurs erreurs standard, les valeurs t et les valeurs P. Les coefficients pour Airport_Distance, Number_of_flights, Weather, Support_Crew_Available, Baggage_loading_time et Late_Arrival_o sont statistiquement significatifs puisque leurs valeurs P sont inférieures à 0.001.
Dans un modèle de régression linéaire, pour une augmentation d’une unité dans les variables prédictives ou indépendantes, cela affichera le changement (augmentation ou diminution) dans le résultat ou la variable dépendante. Cela peut être expliqué comme suit :
Pour chaque augmentation d’une unité dans Number_of_flights, cela augmente l’Arr_Delay de (0.004)
De même pour Support_Crew_Available qu’une diminution d’une unité dans Support_Crew_Available augmente l’Arr_Delay de (-0.05)
De même pour Late_Arrival_o qu’une augmentation d’une unité dans Late_Arrival_o augmente l’Arr_Delay de (7.007)
Le nombre de valeurs ajustées est de 2514 et le nombre d’observations dans l’ensemble de données de formation est également de 2514 ; cela signifie que les valeurs ajustées sont les valeurs prédites de l’ensemble de données de formation.
Prédiction#
Prédire les valeurs ajustées de l’ensemble train_data
Show code cell source
pred_train<- model_sig$fitted.values
head(pred_train)
- 1
- 60.2568422827843
- 3
- 8.64335007903944
- 4
- 98.6611402872728
- 10
- 95.4403625639632
- 11
- 72.9357821621781
- 12
- 104.410995049311
Valeurs résiduelles#
resed_train <- model_sig$residuals
head(resed_train)
- 1
- -2.25684228278431
- 3
- 7.35664992096056
- 4
- -17.6611402872728
- 10
- 26.5596374360368
- 11
- -13.9357821621781
- 12
- 17.589004950689
Les valeurs résiduelles sont la différence entre les valeurs réelles et les valeurs prédites. Si les valeurs réelles sont supérieures aux valeurs prédites, les valeurs résiduelles sont positives et si les valeurs réelles sont inférieures aux valeurs prédites, les valeurs résiduelles sont négatives.
pred_test<- predict(model_sig,newdata = test_data)
head(pred_test)
pred_test1<- data.frame(pred_test)
- 2
- 63.71967746594
- 5
- 66.6435915949123
- 6
- 32.7674359735601
- 7
- 63.250599522936
- 8
- 47.7067054176122
- 9
- 71.1335707505437
Show code cell source
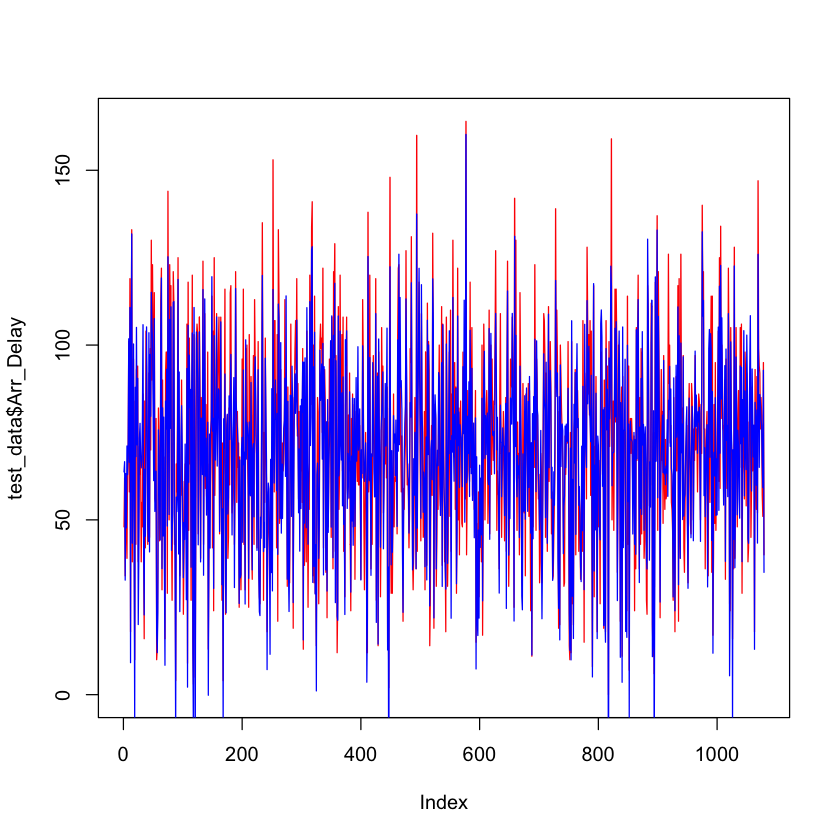
plot (test_data$Arr_Delay,col="red",type ="l",lty=1.8)
lines(pred_test1,col="blue",type ="l",lty=1.4)
La figure ci-dessus présente le graphique des résultats réels par rapport aux résultats prévus. Les lignes rouges représentent les valeurs réelles de l’ensemble des données de test et les lignes bleues représentent les valeurs prédites.
On peut remarquer que la plupart des lignes bleues et rouges se chevauchent, à l’exception de quelques cas. Dans ce cas, on constate que la plupart des valeurs prédites suivent de près les valeurs réelles, ce qui indique qu’il s’agit d’un bon modèle silencieux.