Application: Classification des réclamations d’assurance-vie

Contenu

Application: Classification des réclamations d’assurance-vie#

Introduction#

Dans ce notebook, nous explorerons le concept de classification binaire en utilisant la régression logistique avec R. Nous utiliserons un scénario du secteur de l’assurance : prédire si un titulaire de police d’assurance-vie fera une réclamation dans une période donnée.

1. Configuration de notre environnement#

Nous utilisons tidyverse pour la manipulation des données et la visualisation.
caret nous aidera pour la modélisation et l’évaluation.
pROC sera utilisé pour tracer la courbe ROC.
La définition d’une graine aléatoire garantit que nos processus aléatoires sont reproductibles.

library(tidyverse)
library(caret)
library(pROC)

# Définition du seed aléatoire pour la reproductibilité
set.seed(3035)

── Attaching core tidyverse packages ────────
✔ dplyr     1.1.4     ✔ readr     2.1.5
✔ forcats   1.0.0     ✔ stringr   1.5.1
✔ ggplot2   3.5.1     ✔ tibble    3.2.1
✔ lubridate 1.9.3     ✔ tidyr     1.3.1
✔ purrr     1.0.2     

── Conflicts ─────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors

Loading required package: lattice

Attaching package: ‘caret’

The following object is masked from ‘package:purrr’:

    lift

Type 'citation("pROC")' for a citation.

Attaching package: ‘pROC’

The following objects are masked from ‘package:stats’:

    cov, smooth, var

2. Génération de données synthétiques#

Dans un scénario réel, vous chargeriez généralement des données à partir d’un fichier csv par exemple read.csv ou d’une base de données. Pour cet exemple, nous allons créer des données synthétiques pour imiter les informations réelles des titulaires de polices d’assurance.

n <- 1000
donnees <- tibble(
  age = runif(n, 20, 70),
  imc = rnorm(n, 25, 5),
  tension_arterielle = rnorm(n, 120, 15),
  cholesterol = rnorm(n, 200, 30),
  fumeur = sample(c("oui", "non"), n, replace = TRUE, prob = c(0.2, 0.8)),
  antecedents_familiaux = sample(c("oui", "non"), n, replace = TRUE),
  frequence_exercice = sample(c("faible", "moyenne", "elevee"), n, replace = TRUE)
)

Nous avons créé un jeu de données avec 1000 titulaires de polices, chacun avec diverses caractéristiques de santé et de style de vie.

La variable “reclamation” est notre cible. Elle est binaire (0 ou 1) et représente si un titulaire de police a fait une réclamation.

donnees <- donnees %>%
  mutate(
    proba_reclamation = 0.01 +
      0.001 * (age - 20) +
      0.02 * (imc - 25) +
      0.002 * (tension_arterielle - 120) +
      0.001 * (cholesterol - 200) +
      0.1 * (fumeur == "oui") +
      0.05 * (antecedents_familiaux == "oui") +
      -0.05 * (frequence_exercice == "elevee"),
    reclamation = rbinom(n, 1, proba_reclamation)
  ) %>%
  select(-proba_reclamation)

Warning message:
“There was 1 warning in `mutate()`.
ℹ In argument: `reclamation = rbinom(n, 1,
  proba_reclamation)`.
Caused by warning in `rbinom()`:
! NAs produced”

print(head(donnees))

# A tibble: 6 × 8
    age   imc tension_arterielle cholesterol fumeur antecedents_familiaux
  <dbl> <dbl>              <dbl>       <dbl> <chr>  <chr>                
1  30.5  25.6               97.5        161. oui    oui                  
2  66.0  27.3              136.         197. non    non                  
3  51.0  17.8               99.5        222. non    non                  
4  46.7  19.8              138.         213. non    oui                  
5  43.7  30.2              113.         191. oui    oui                  
6  37.8  19.9              143.         149. oui    oui                  
# ℹ 2 more variables: frequence_exercice <chr>, reclamation <int>

print(paste("Dimensions des données :", paste(dim(donnees), collapse = " x ")))

[1] "Dimensions des données : 1000 x 8"

Nous avons généré “reclamation” en fonction d’une probabilité influencée par d’autres caractéristiques, en ajoutant un peu d’aléatoire pour imiter la complexité du monde réel.

3. Analyse exploratoire des données#

Avant de construire notre modèle, il est crucial de comprendre nos données.

Statistiques de base#

summary(donnees)

      age             imc         tension_arterielle  cholesterol   
 Min.   :20.06   Min.   : 7.216   Min.   : 76.18     Min.   :101.0  
 1st Qu.:32.11   1st Qu.:21.839   1st Qu.:109.38     1st Qu.:180.1  
 Median :44.55   Median :25.047   Median :120.11     Median :201.0  
 Mean   :44.99   Mean   :24.996   Mean   :119.70     Mean   :200.6  
 3rd Qu.:58.25   3rd Qu.:28.078   3rd Qu.:129.56     3rd Qu.:221.0  
 Max.   :69.99   Max.   :43.790   Max.   :162.91     Max.   :285.5  
                                                                    
    fumeur          antecedents_familiaux frequence_exercice  reclamation   
 Length:1000        Length:1000           Length:1000        Min.   :0.000  
 Class :character   Class :character      Class :character   1st Qu.:0.000  
 Mode  :character   Mode  :character      Mode  :character   Median :0.000  
                                                             Mean   :0.113  
                                                             3rd Qu.:0.000  
                                                             Max.   :1.000  
                                                             NA's   :310    

Carte de chaleur des corrélations#

donnees %>%
  select(where(is.numeric)) %>%
  cor() %>%
  heatmap(Rowv = NA, Colv = NA, scale = "none", margins = c(10, 10))

../../_images/1cbbfd8dba81d50fe2b615e6b536a23b0fc80b9507a9fc2823fdc1a0e6345f85.png

Distribution des réclamations#

ggplot(donnees, aes(x = factor(reclamation))) +
  geom_bar() +
  labs(title = "Distribution des réclamations d'assurance", x = "Réclamation", y = "Nombre")

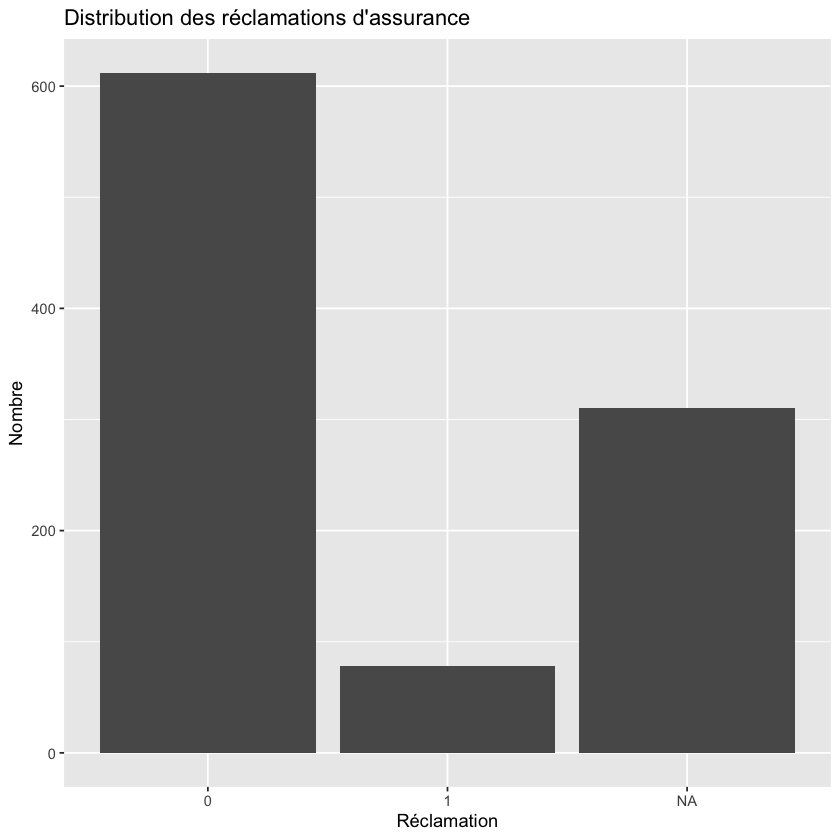
../../_images/2151d14925e9482ea65ef9163b4592ac33abeb96ff98fc47dbaa2d56e0cc39fc.png

Nuage de points âge vs IMC, coloré par statut de réclamation#

ggplot(donnees, aes(x = age, y = imc, color = factor(reclamation))) +
  geom_point(alpha = 0.6) +
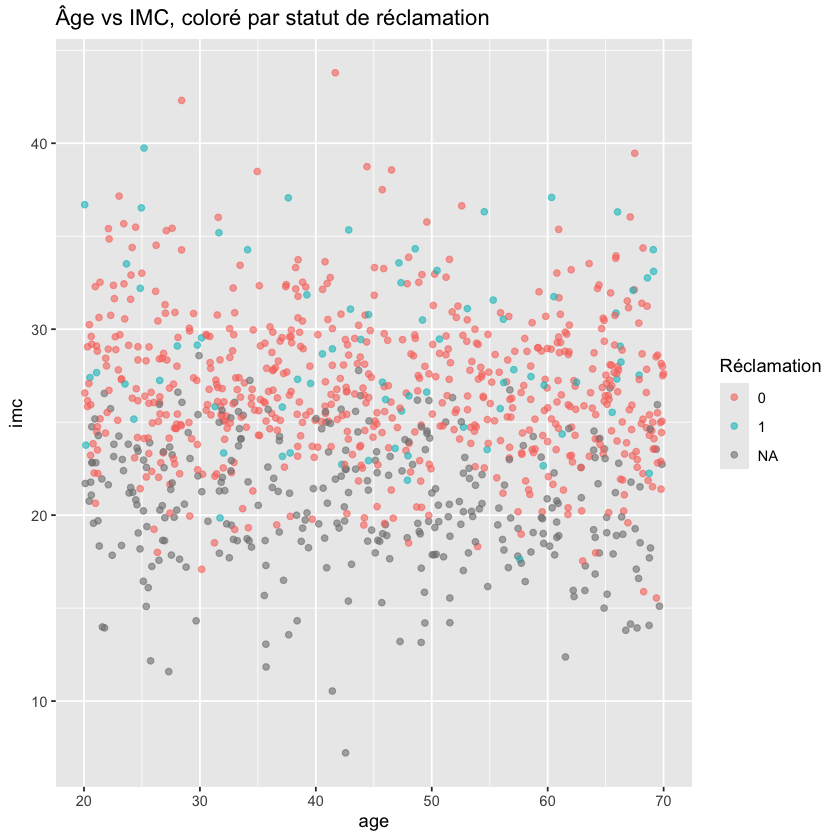
  labs(title = "Âge vs IMC, coloré par statut de réclamation", color = "Réclamation")

../../_images/2bcce681d3ada2823aaf60a59e0c64ef859f464e2d88ff513d63b25ca0ac8cea.png

La fonction summary() nous donne un aperçu rapide de nos caractéristiques.
La carte de type « heat map » des corrélations nous aide à visualiser les relations entre les caractéristiques numériques.
Nous traçons la distribution des réclamations pour vérifier le déséquilibre des classes.
Le nuage de points de l’âge par rapport à l’IMC, coloré par le statut de réclamation, peut révéler des tendances dans ces variables clés

4. Prétraitement des données#

Maintenant, préparons nos données pour le modèle de régression logistique.

# Conversion des variables catégorielles en variables indicatrices
donnees_encodees <- donnees %>%
  mutate(across(where(is.character), as.factor))
# donnees <- donnees %>% filter(!is.na(reclamation))
# Séparation des caractéristiques et de la cible (variable réponse)
X <- donnees_encodees %>% select(-reclamation)
y <- donnees_encodees$reclamation

# Division en ensembles d'entraînement et de test
indices_partition <- sample(1:length(y), size = floor(0.8 * length(y)))
X_train <- X[indices_partition, ]
X_test <- X[-indices_partition, ]
y_train <- y[indices_partition]
y_test <- y[-indices_partition]

print(paste("Dimensions de l'ensemble d'entraînement :", paste(dim(X_train), collapse = " x ")))
print(paste("Dimensions de l'ensemble de test :", paste(dim(X_test), collapse = " x ")))

[1] "Dimensions de l'ensemble d'entraînement : 800 x 7"

[1] "Dimensions de l'ensemble de test : 200 x 7"

Nous convertissons les variables catégorielles en facteurs.
Nous séparons nos caractéristiques (X) de notre variable cible (y).
Nous divisons nos données en ensembles d’entraînement (80%) et de test (20%). L’ensemble d’entraînement est utilisé pour construire le modèle, tandis que l’ensemble de test est utilisé pour évaluer sa performance.

5. Construction du modèle de régression logistique#

Nous sommes maintenant prêts à créer et à entraîner notre modèle de régression logistique.

modele <- glm(reclamation ~ ., data = cbind(X_train, reclamation = y_train), family = binomial())

summary(modele)

Call:
glm(formula = reclamation ~ ., family = binomial(), data = cbind(X_train, 
    reclamation = y_train))

Coefficients:
                            Estimate Std. Error z value Pr(>|z|)    
(Intercept)               -12.263322   2.095806  -5.851 4.88e-09 ***
age                         0.017928   0.010065   1.781   0.0749 .  
imc                         0.172280   0.033699   5.112 3.18e-07 ***
tension_arterielle          0.013727   0.010317   1.330   0.1834    
cholesterol                 0.008581   0.004733   1.813   0.0699 .  
fumeuroui                   0.534501   0.329163   1.624   0.1044    
antecedents_familiauxoui    0.732968   0.310931   2.357   0.0184 *  
frequence_exercicefaible    0.581082   0.395529   1.469   0.1418    
frequence_exercicemoyenne   0.686371   0.388789   1.765   0.0775 .  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 378.14  on 545  degrees of freedom
Residual deviance: 336.93  on 537  degrees of freedom
  (254 observations deleted due to missingness)
AIC: 354.93

Number of Fisher Scoring iterations: 5

6. Évaluation du modèle#

Évaluons maintenant la performance de notre modèle.

# Faire des prédictions sur l'ensemble de test
y_pred <- predict(modele, newdata = X_test, type = "response")
y_pred_class <- ifelse(y_pred > 0.5, 1, 0)

# Matrice de confusion
conf_matrix <- confusionMatrix(factor(y_pred_class), factor(y_test))
print(conf_matrix)

# Courbe ROC
courbe_roc <- roc(y_test, y_pred)
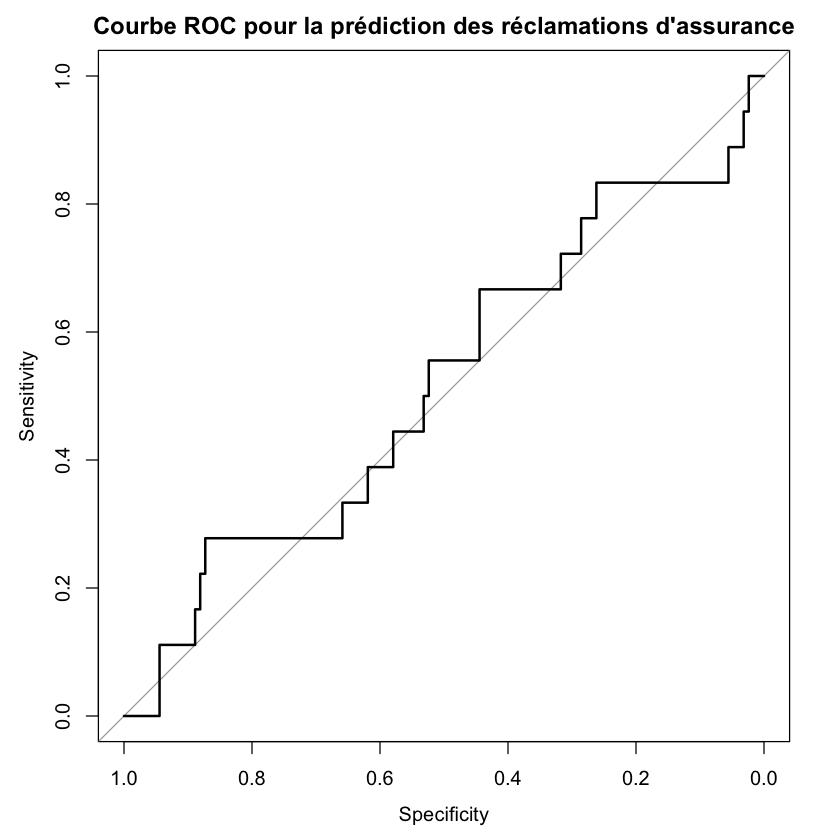
plot(courbe_roc, main = "Courbe ROC pour la prédiction des réclamations d'assurance")
auc(courbe_roc)

Warning message in confusionMatrix.default(factor(y_pred_class), factor(y_test)):
“Levels are not in the same order for reference and data. Refactoring data to match.”

Confusion Matrix and Statistics

          Reference
Prediction   0   1
         0 126  18
         1   0   0
                                          
               Accuracy : 0.875           
                 95% CI : (0.8097, 0.9242)
    No Information Rate : 0.875           
    P-Value [Acc > NIR] : 0.5624          
                                          
                  Kappa : 0               
                                          
 Mcnemar's Test P-Value : 6.151e-05       
                                          
            Sensitivity : 1.000           
            Specificity : 0.000           
         Pos Pred Value : 0.875           
         Neg Pred Value :   NaN           
             Prevalence : 0.875           
         Detection Rate : 0.875           
   Detection Prevalence : 1.000           
      Balanced Accuracy : 0.500           
                                          
       'Positive' Class : 0               
                                          

Setting levels: control = 0, case = 1

Setting direction: controls < cases

0.517195767195767

../../_images/4db852954d34796c5ae8d285ac3bd3f8f6a5e3d85f5ad9eb457aeafb200c08d0.png

La matrice de confusion nous montre les vrais positifs, vrais négatifs, faux positifs et faux négatifs du modèle.
La courbe ROC (Receiver Operating Characteristic) trace le taux de vrais positifs par rapport au taux de faux positifs à différents seuils. L’aire sous la courbe (AUC) est une mesure du pouvoir prédictif du modèle.

7. Faire des prédictions#

Enfin, utilisons notre modèle pour faire des prédictions pour de nouveaux titulaires de polices.

predire_probabilite_reclamation <- function(age, imc, tension_arterielle, cholesterol, fumeur, antecedents_familiaux, frequence_exercice) {
  nouvelles_donnees <- tibble(
    age = age,
    imc = imc,
    tension_arterielle = tension_arterielle,
    cholesterol = cholesterol,
    fumeur = factor(fumeur, levels = levels(X_train$fumeur)),
    antecedents_familiaux = factor(antecedents_familiaux, levels = levels(X_train$antecedents_familiaux)),
    frequence_exercice = factor(frequence_exercice, levels = levels(X_train$frequence_exercice))
  )
  
  predict(modele, newdata = nouvelles_donnees, type = "response")
}

proba <- predire_probabilite_reclamation(45, 28, 130, 220, "non", "oui", "moyenne")
print(paste("La probabilité que ce titulaire de police fasse une réclamation est de :", round(proba, 4)))

[1] "La probabilité que ce titulaire de police fasse une réclamation est de : 0.1764"

Nous avons créé une fonction qui prend les informations d’un nouveau titulaire de police et renvoie la probabilité qu’il fasse une réclamation.
Cette fonction prétraite les données d’entrée de la même manière que nos données d’entraînement, assurant ainsi la cohérence.
Le résultat est une probabilité entre 0 et 1, qui peut être utilisée pour prendre des décisions ou évaluer le risque.

Conclusion#

Dans ce notebook, nous avons parcouru l’ensemble du processus de construction d’un modèle de régression logistique pour prédire les réclamations d’assurance en utilisant R. Nous avons couvert la préparation des données, l’analyse exploratoire, la construction du modèle, l’évaluation et l’application pratique.